출처: 2022 수능특강 미적분

Laplace Transform

Laplace Transform
$$F(s)=L\{f\} = \int_0^\infty f(t)e^{-st}dt$$

쉽게 말하면 $t$에 대한 함수 $f(t)$를 $s$에 대한 함수 $F(s)$로 나타내는 것.
공학수학, 미분방정식 등 여러 과목에서 소개하고 이공계 전반에 걸처 푸리에 변환과 같이 자주 쓰이는 변환

근데 물리학과에서는 푸리에 변환을 훨씬 자주 쓰는듯
어차피 둘이 똑같은 꼴이기는 하지만 기저에 깔린 철학이 좀 달라서 쓰임새도 좀 달라요

라플라스 변환표

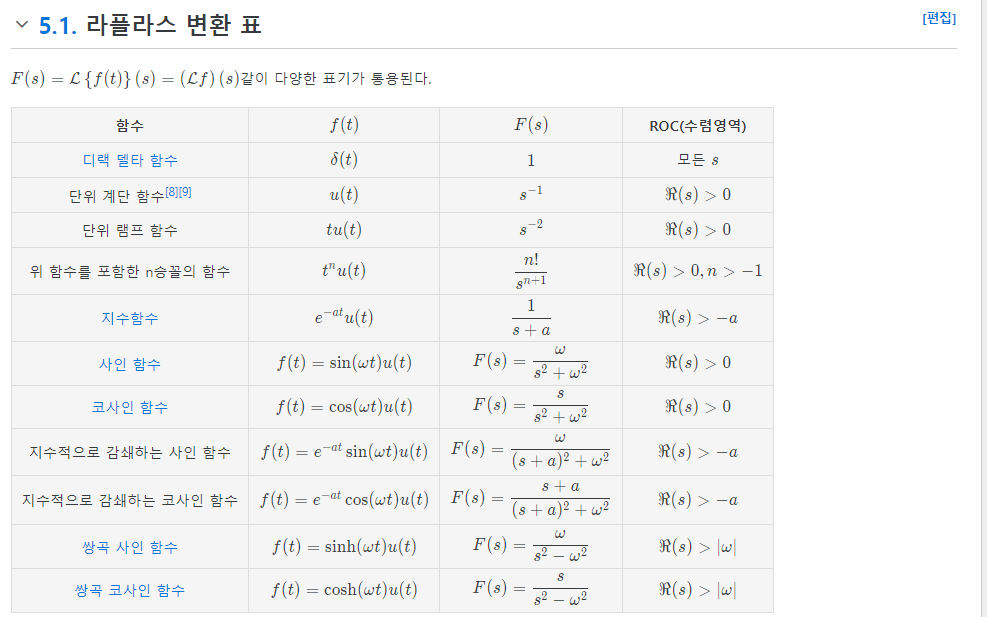
출처: 나무위키
Q. 왜 저렇게 변환이 되는가?
A. 직접 라플라스 변환 정의 이용해서 열심히 식 정리하면 저렇게 나온다. 직접 그걸 정리하기란 매우 귀찮은 일이므로 변환표 참고하는 게 훨씬 빠르다.

Convolution

합성곱, Convolution 연산은 아래와 같이 정의한다. 두 함수 $f, g$에 대해 합성곱 연산 $*$을 적용하면 아래와 같다. 참고로 컨볼루션 연산인지 아닌지 빠르게 판단하는 방법은, 적분식 안에 두 함수가 들어있는데 두 함수의 인자가 더했을 때 일정하면 콘볼루션이다.

$$(f*g)(t)=\int_0^t f(t-u)g(u)du$$

라플라스 변환표에 없는 것 같아 추가 서술하자면, $L\{f*g\}=L\{f\}L\{g\}$이다. 다시 말해 합 성곱 연산 후에 라플라스 변환을 한 결과는 라플라스 변환 후 곱한 결과와 같다. (FFT를 통해 다항식의 빠른 곱셈을 하는 것과 같은 원리)

수특 문제 풀이

수특 문제의 $\int_0^t f(t)\sin(x-t)dt$는 $f * \sin$와 같다.

수특 문제의 함수에 라플라스 변환 적용하면
$$F(s)=\dfrac{s}{s^2+1}-2F(s)\dfrac{1}{s^2+1}$$

이제 그냥 $F(s)$에 대해 정리하면 된다. 그냥 단순 식정리다.
$$F(s)=\dfrac{s}{s^2+3}$$

라플라스 변환표를 보면 $\cos{\sqrt{3} t}$과 구한 $F(s)$가 똑같다. 따라서 함수 $f(x)=\cos \sqrt{3}x$이다.

ㄱ, ㄷ 보기는 매우 자명하게 풀리고 ㄴ 보기도 좌변=우변=0 나와서 맞아야만 하는데 정답은 틀 리다 나와서 왜 그런가 싶었는데.. 답지를 보니

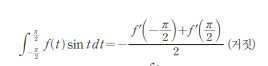
$0\ne -0$이라 ㄴ이 틀렸다고 주장하는 수능특강
이게 수능특강 클라스..? 라는 생각이 잠깐 들었으나

다행히 정오표에는 제대로 나와있다.