1. \(y(x,t)\)란?

$$y(x,t)=A\sin(\omega t-kx)$$

\(\omega t, kx\)는 무차원임을 숙지하고 있으면 좋다. (사인에 들어가는 값은 차원이 없어야 한다. 후술할 위상차 \(\phi\)도 마찬가지이다.) 이 사실을 기억하고 있으면 \(t\)차원을 알면 \(\omega\)차원을 알 수 있고, \(x\)차원을 알면 \(k\)차원을 알 수 있다.

\(y(x,t)\)는,

진동수 \(\omega\) (주기 \(T=\frac{2 \pi}{\omega}\)),

파수 k (파장 \(\lambda =\frac{2\pi}{k}\)),

진폭 \(A\)의 사인파형 파동을 정량적으로 표현하고 있다. (편의상 \(A>0\)이라 하겠다) 매우 깔끔하다는 생각이 들지 않는가?

참고로 사인 내부 항이 \(k\lambda\) 변하는 것은 한 파장 이동함을 뜻하고, 이것은 사인안에 들어가는 항이 \(2\pi\)변함을 뜻한다. 따라서 \(k\lambda=2\pi, \lambda=\frac{2\pi}{k}\)이다. 이런 방식으로 \(\omega\)와 \(t\)의 관계, \(k\)와 \(x\)의 관계 등을 외우면 편하다.

사실은 \(y(0,0)=0\)인 경우만 있지는 않으므로 \(\phi\) term을 위상에 더해 \(y(x,t)=A\sin(\omega t-kx+\phi)\)로 나타내기도 한다.

혹시나 \(y(x,t)\)가 이해가 잘 안 간다면 진동수, 파수, 시간, 위치 등에 적당한 숫자를 정해 숫자를 직접 넣어보자.

2. 파동의 중첩(진폭이 같을 때 위주로)

이제 파동 2개를 합쳐보자.

$$y_1(x,t)=A_1\sin(kx-\omega t)\\y_2(x,t)=A_2\sin(kx-\omega t+\phi)\\y \prime(x,t)=y_1(x,t)+y_2(x,t)$$

만약 \(A_1=A_2\)라면 (진폭 동일) 아래와 같이 합성파를 표현할 수 있다. 왜 합쳐서 아래와 같은 꼴이 나오는지는 특별한 이유가 있는 건 아니고 그냥 단순히 수식 정리의 결과일 뿐이다.

$$y\prime(x,t)=2A\cos(\frac{\phi}{2})\sin(kx-\omega t+\frac{\phi}{2})$$

위 수식을 참고하면, 합성파에서는, \(A\prime=2A\cos(\frac{\phi}{2})\)을 진폭으로 취급할 수 있다. 위상차 \(\phi\)가 상수니까. (여기서 잠깐, 물리학1에서 대충 "골골이거나 마루마루면 위상이 같고 골마루면 위상이 반대다" 라고 설명했던 그 "위상차"를 어떻게 보면 좋을 지 파악할 수 있다. 매우 단순하게, 사인 안에 들어간 값의 차이라고 보면 된다.)

그러면, \(\phi\)가 \(\pi\)의 짝수배면 보강간섭, 홀수배면 상쇄간섭이 일어난다는 것을 알 수 있다.

\(y_1, y_2\)를 각각 관찰하면서 풀어서 말하면 \(\phi=2n\pi\)면 \(y_1, y_2\)가 같은 위상으로 만나서 보강간섭이 일어나며

\(\phi=(2n-1)\pi\)면 \(y_1, y_2\)가 반대 위상으로 만나서 상쇄간섭이 일어나는 것이라 해석할 수 있다.

예제

양쪽 파원에서 물결파가 발생하는데 경로차가 어떻게 되야 보강간섭이 발생하는지 파악하는 문제를 예로 들어보자. 파원에서 위상차 없이 파동이 발생한다고 가정하면 경로차(\(x\)의 차이)를 따지라는건데, \(kx=2n{\pi}\)를 \(k=\frac{2\pi}{\lambda}\)로 양변을 나누면 \(x=2n\frac{\lambda}{2}\)가 되어, 파장/2의 짝수배만큼 경로차가 나면 보강간섭이 난다는 익히 알던 그 명제를 유도할 수 있다.

그럼, 이제 두 파원에서 위상차가 날 때는 보강간섭 조건이 어떻게 바뀔지는 독자가 직접 해보면 좋을 듯하다. 경로차는 뭐고 위상차와는 어떻게 다른지(위에서 이미 힌트는 다 줬지만)도 한번쯤 고민해보자.

유의사항, 오개념

참고로 보강간섭은 \(t\)를 고정해 놓고 따지는 게 아니다. \((x,t)\), 아니면 최소한 \(x\)를 정해 놓고 따져야 한다. 어떤 시점 \(t=t_0\)에서(어떤 시점에) 파동의 전체 사진, 변위-위치 그래프를 가지고 변위=0인 점은 무조건 상쇄간섭이겠지? 이렇게 따지면 안 된다. 비슷한 맥락에서 생기는 오개념이 또 있는데, 보강간섭하는 지점이라고 항상 변위가 0이 아닌 것이 아니다. 보강간섭하는 지점은 진폭이 2A인거지 변위가 항상 2A나 -2A로 불연속적으로 이동하는 게 아니다. \(y=2A\sin(\omega t)\)는 시간에 상관없이 \(y=2A,-2A\)임을 뜻하지 않는다.

3. 그래프와 연관지어 해석

변위-위치 그래프는 y축이 y(x,t), x축이 x이며

변위-시간 그래프는 y축이 y(x,t), x축이 t인 그래프라 할 수 있다.

전자는 t가 고정, 후자는 x가 고정됨을 전제로 하고 있을 것이다. 각각의 그래프에서 알아낼 수 있는 게 왜 각각 파장과 주기인지, y(x,t)를 나타내는 수식에서 상수와 변수를 적절히 구분한 후 생각해보자.

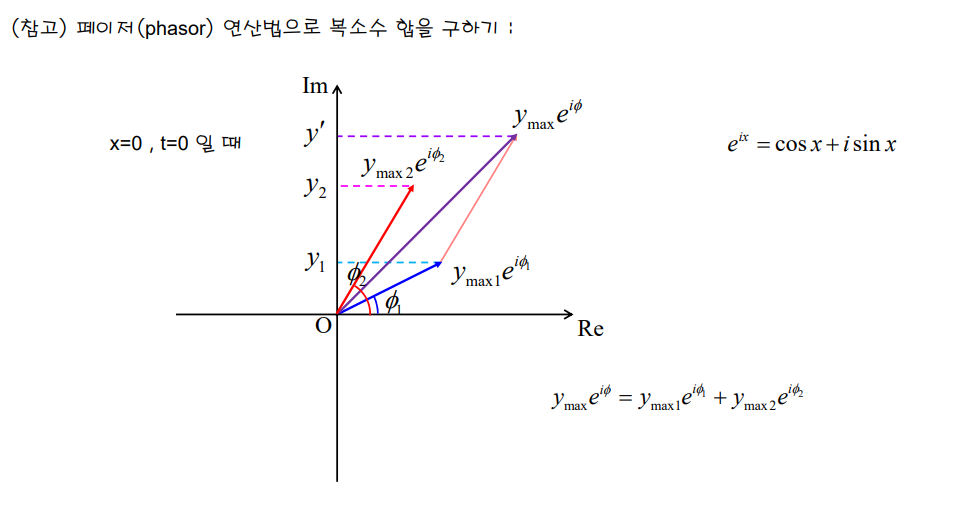
참고(물리학1 바깥) - 진폭이 다를 때 중첩방법

출처: 서울대학교 2021 여름 계절학기 물리학1 수업자료