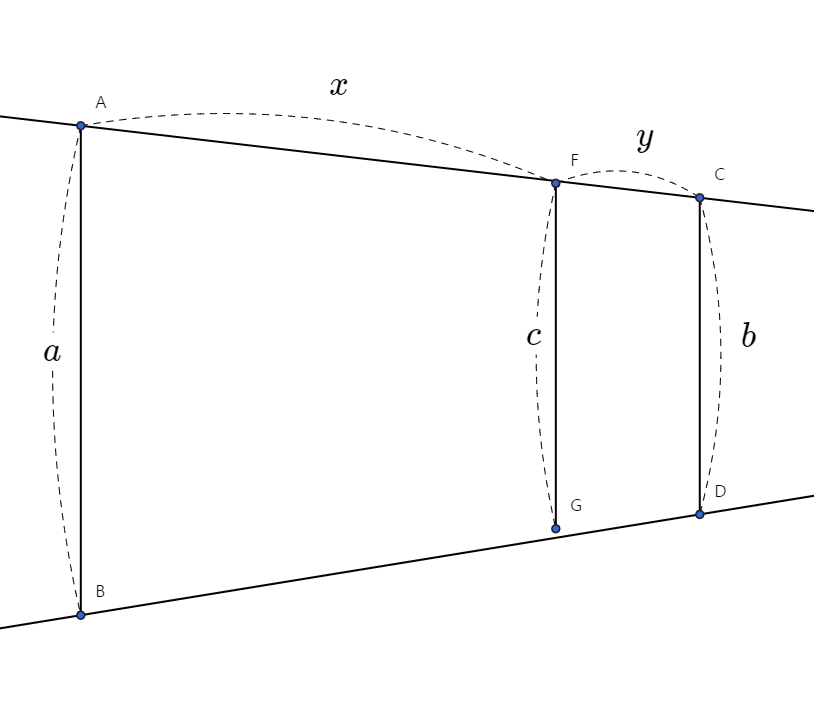
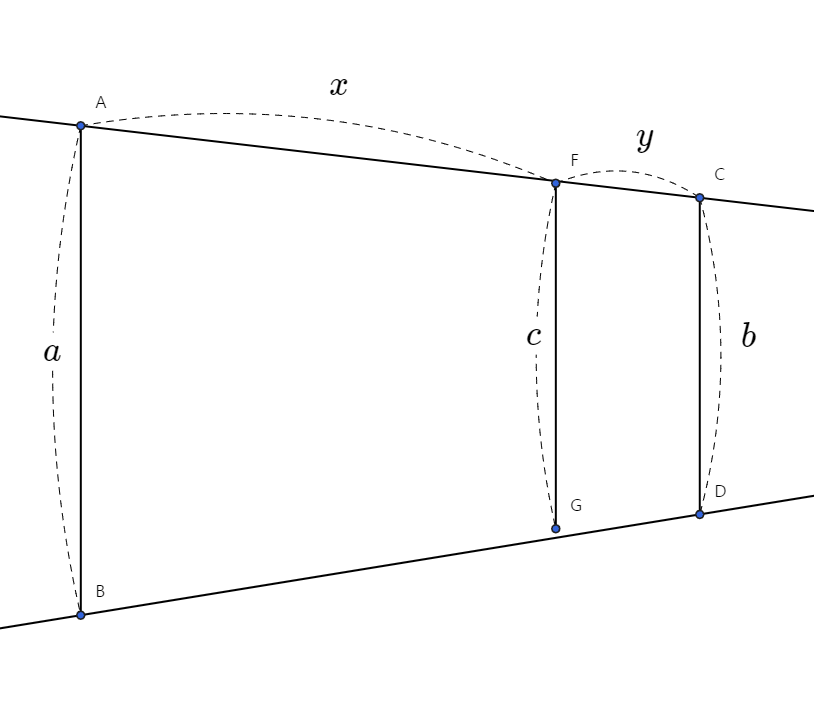
여기서 $c$는 얼마일까?

결론부터 말하면,

\[c=\frac{y}{x+y}a+\frac{x}{x+y}b\]

즉 $c$는 $a,b$의 가중합으로 나타내어지는데, 특히 그 가중치는 해당 선분에서 반대편에 있는 $y,x$의 비율에 따라 나타내어진다.

이유

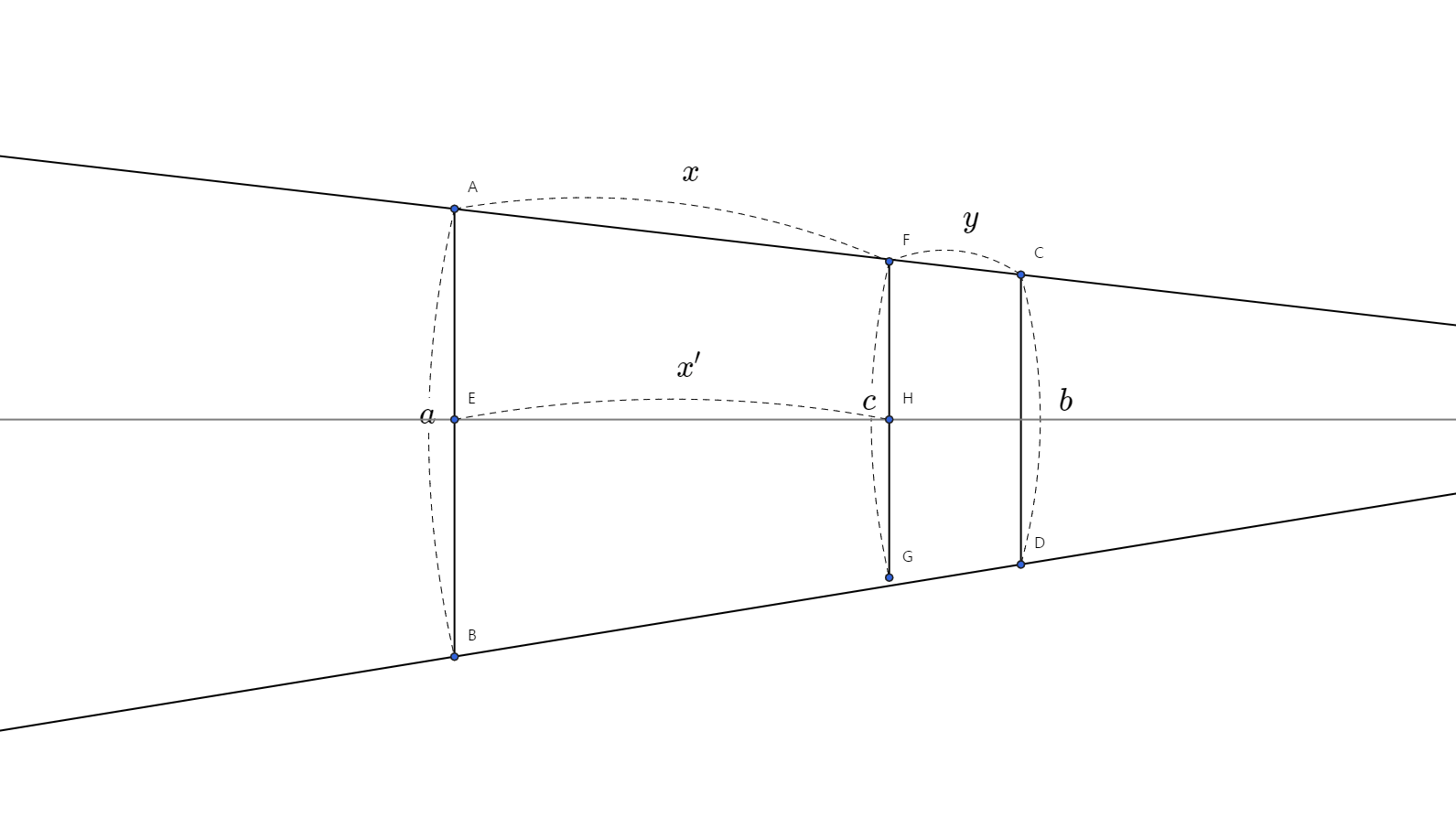
직선 AC와 직선 BD가, 말 그대로 "직선"이므로(만약 곡선이거나 했다면 결과가 달랐을 것) 선분 AB에서 $x^\prime$만큼 이동하면, $kx^\prime$만큼 선분 길이가 줄어든다. (FG 선분 길이와 AB 선분 길이를 비교해보자)

다시 말해, AB에서 이동한 거리와 선분 길이의 변화량이 비례한다.

AB에 대해 사다리꼴 안에서 가장 멀리 이동하면 CD가 되고, $a-b$만큼 선분 길이가 줄어든다. 만약 AB에서 CD 거리의 절반만큼 AB에서 이동하면 $\frac{a-b}{2}$만큼 선분 길이가 줄어든다. ($c=\frac{a+b}{2}$라는 나름 잘 알려진 공식이 나온다) 만약 AB에서 CD 거리의 1/3만큼 AB에서 이동하면 $\frac{a-b}{3}$만큼 선분 길이가 줄어든다.

이런 식으로 생각하면 $a,b$의 가중합으로 $c$를 나타낼 수 있다고 파악할 수 있다.

극단적인 경우로 AB에서 0만큼 이동하면 $c=a \cdot \frac{1}{1}+b \cdot\frac{0}{1}=a$, AB에서 CD까지 이동하면 $c=a \cdot \frac{0}{1}+b \cdot\frac{1}{1}=b$가 된다.

사다리꼴 외부로 벗어나서도 공식이 성립할 것이라 파악할 수 있다. 또한, 특히 직선 AC와 BD가 평행하다면 $k=0$이 되어 선분 AB에서 멀어져도 선분 길이가 변하지 않을 것이다.

이유 보충설명

위에 적은 논리가 좀 직관적인 면이 있어 보충설명하자면

x축(대충 EH를 연장한 직선을 x축으로 삼자)을 따라 이동한 거리 $x^\prime$에 따라, $x=x^\prime$에 수직한, 사다리꼴을 이루는 선분의 길이는 $ax^\prime+b$ 꼴로 나타내어진다.

$y=ax+b$ 그래프를 좌표평면에 그려보면 좀 더 이해가 잘 갈지 모르겠는데, 사다리꼴 양옆 선분 길이를 안다는 것은 $y=ax+b$ 그래프의 두 점을 알고 있다는 말(=직선이 하나로 확정됨)이다. 그리고 $y=ax+b$ 직선 위의 한 점은 두 점을 잇는 선분 내의 내분점(또는 외분점)으로 표현이 된다.

그래서 사다리꼴 양옆 선분 길이의 내분(또는 외분) 꼴로 중간 선분 길이를 나타낼 수 있다.