테이블 적분법

보통 LIATE(로그함수-역삼각함수-대수적함수-삼각함수-지수함수), 또는 고등학교에서는 로다삼지(로그함수,다항함수,삼각함수,지수함수)라고 한다. 오름차순으로 적분이 쉽고, 내림차순으로 미분이 쉽다. 논술 문제 중 적용이 안 되는 것들이 몇 있지만 수능에서는 대부분 적용된다.

아무튼 부분적분할 때 특히 이러한 LIATE 순서를 활용하면 쉽다. 근데 부분적분에 있어서 꽤 유용한 테이블 적분법을 아는 친구가 별로 없어서 블로그에 적어본다.

1. 미분하기 쉬운 함수를 왼쪽, 적분하기 쉬운 함수를 오른쪽에 적는다.
2. 왼쪽에 적은 함수를 적당한 만큼 여러 번 미분해서 아래로 늘여 적는다.
3. 오른쪽에 적은 함수를 적당한 만큼 여러 번 적분해서 아래로 늘여 적는다.
4. 짝수번째 행마다 - 를 붙인다. 보통 왼쪽 함수 왼쪽에 적는다. 헷갈리지 않도록 왼쪽 함수에 붙여서 적지는 않는다.
5. 대각선 방향으로 곱하면서 나온 항들을 전부 더한다. 이 때 짝수번째 항마다 붙여준 -도 곱해줘야 한다.
6. 그러면 2가지 경우가 생긴다. 첫번째 경우, xsin (x)와 같은 함수는 x를 왼쪽에 적고 미분하다 보면 0이 되버린다. 그러면 0이 나올 때부터는 안 더해도 같은 결과가 나온다.
7. 두번째 경우, 미분을 여러 번 하기 힘들거나 미분해도 0이 안 나오거나 그런 경우에는 중간에 대각선으로 곱하지 말고 같은 행에 있는, 왼쪽의 함수와 오른쪽의 함수를 곱하고, 그것에 적분기호를 씌우고 지금까지의 결과에 더한다.

상수항이 나오는 경우는, 이러한 경우이다.

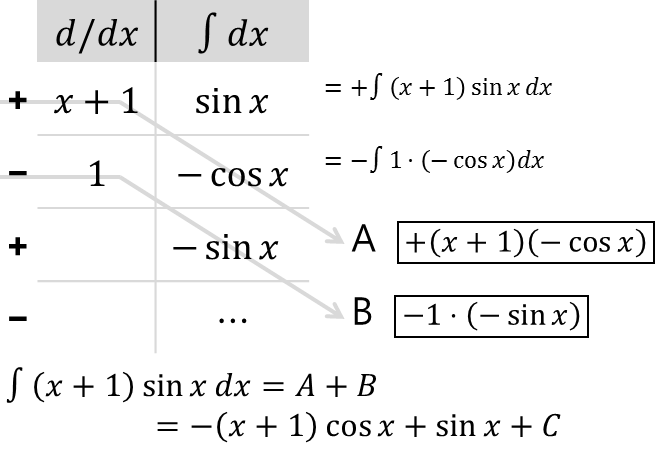
다른 예제로, f(x) = sin x ⋅ ex를 적분한다고 해보자.

$$\begin{array}{ccc} D && I\\ \hline \sin x&{}&e^x\\ {}&\searrow{+}&{}\\ \cos x&{}&e^x\\ {}&\searrow{-}&{}\\ -\sin x&{\rightarrow{+}}&e^x\\ \end{array}$$

$$\int \sin x\cdot e^xdx=+(\sin x\cdot e^x)-(\cos x\cdot e^x)+{\int(-\sin x)\cdot e^x dx}$$

그럼 우변의 ∫sin x ⋅ exdx를 좌변으로 넘기고 계산하면 된다.