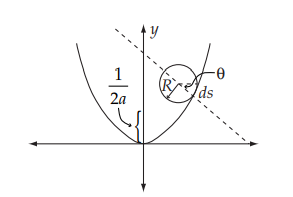
별 내용은 아닌데.. 그냥 제가 고등학생 때 이걸 논술 문제로 처음 접했었는데 되게 신기하다고 느꼈던 기억이 나서 간단히 적어봅니다. 칼럼의 주제는 "포물선 위를 구르는 원이 포물선과 하나의 교점만 가질 조건"이고, 풀이는 곡률의 개념을 이용해 진행할 예정입니다. 미리 말하지만 당연히 교과외이고 그냥 궁금한 사람은 이런 게 있구나 하고 읽고 넘어가면 됩니다.

고등학생 때 저는 곡률이 뭔지 몰라서 열심히 수식으로 노가다해서 어 이때는 교점 개수가 달라질 수 있네.. 이 때는 안 달라지 네.. 근데 왜 그런지 모르겠네.. 이렇게 풀었던 기억이 나서, 그런 학생들에게 직관적으로 이 문제를 이해하는 데 도움이 될 겁 니다. 궁금한 사람은 한번 풀어보세요.

문제

방금 Marion 역학 6-11 문제를 풀다 칼럼 써볼 생각이 났던건데, 마리온 역학 책을 참고할 필요는 당연히 없고, 문제를 요약하자면 "$y=ax^2$의 포물선이 있고 이 위를 굴러가는 원이 있으면 원의 위치와 상관없이 원과 포물선이 하나의 교점만을 가질 조건은 무엇인가?" 입니다.

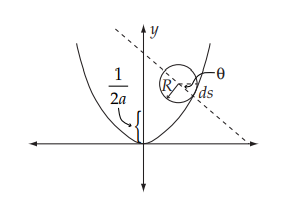
해설

결론부터 말하면 답은 다음과 같습니다.
$y=ax^2$이면, $R\le \frac{1}{2a}$여야 항상 교점을 하나만 가지고, 그렇지 않다면 원의 위치에 따라 교점을 1개보다 많이 가질수도, 하나 가질수도 있습니다. (Marion 해설에는 $R$ 조건에 등호가 들어있지 않던데, 혹시 등호가 안 들어가는 게 맞다면 지 적 부탁드립니다.)

고등학생 때 포물선과 원이 가지는 교점이 가지는 교점을 세라고 했을 때, 원의 반지름이나 포물선의 초점거리에 따라 교점 개수가 항상 하나일수도 있고 하나에서 3개로 변할수도 있다는 게 되게 신기했던 기억이 납니다. 이 이유를 곡률을 이용해 설명해보 겠습니다.

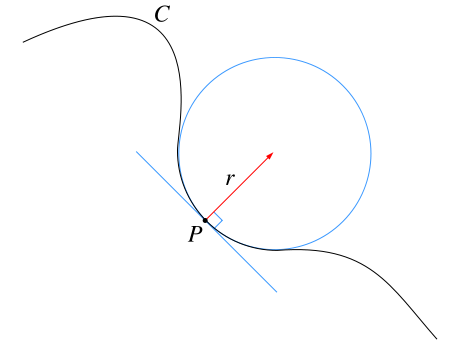
곡선은 어떤 한 점에서 미분계수를 구할 수 있습니다. (그런 곡선만을 대상으로 논의를 진행하겠습니다.) 당연히 접선도 구할 수 있습니다. 곡선 위의 어느 한 점에 대해 접선에 수직이며 접점을 지나는 원은 여러개인데, '접촉원'이란 아래 그림과 같이 원과 곡선의 (P가 아닌) 교점들을 P로 극한 보낼 때 나오는 원을 말합니다.

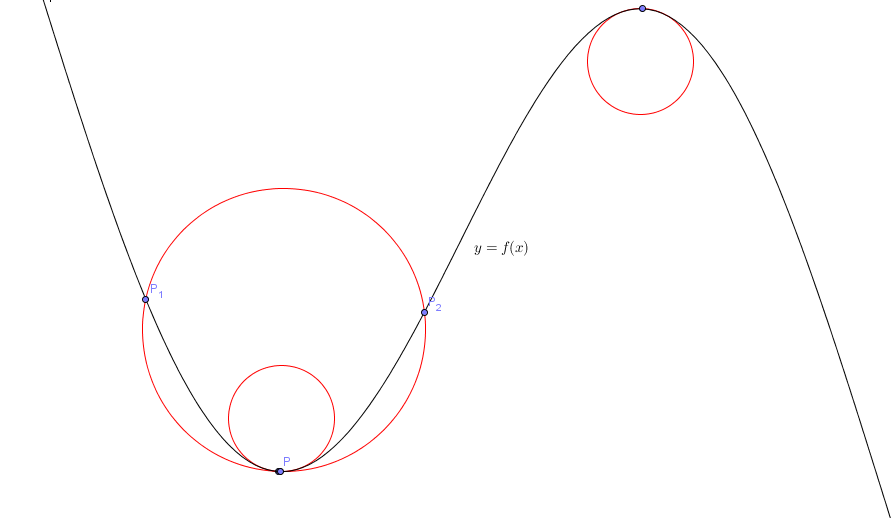
곡선의 곡률은, 정의하는 방식이 여럿 있지만, 접촉원의 반지름의 역수 $\frac{1}{r}=\kappa$로 정의할 수도 있습니다. 또한 곡 률 $\kappa$은 2차원상에서 수식으로 다음과 같이 유도되는데, 유도 과정은 고교 과정 내용도 아니고 궁금한 사람은 고등학생이 라도 찾아보면 이해하기 어렵지 않으니 생략하겠습니다. 궁금한 사람은 접촉원과 곡률, 대학 교 미적분학 책(미적분학2+) 등을 참고하면 됩니다.

$$\kappa=\dfrac{|y''x'-x''y'|}{(x'^2+y'^2)^{\frac{3}{2}}}$$

$y=ax^2$에 대해 곡률을 구하면,

$$ \kappa=\dfrac{|y''x'-x''y'|}{(x'^2+y'^2)^\frac{3}{2}}=\dfrac{2a}{(1+(2ax)^2)^\frac{3}{2}} $$
이는 x=0에서 최댓값 $2a$을 가지며 x가 무한대로 갈 때 0으로 갑니다.

따라서 접촉원의 반지름은 x=0에서 최소 $\frac{1}{2a}$, x가 무한대로 갈 때 무한히 커집니다.

$y=ax^2$의 어느 한 점에서 접하는 원이, 그 점에서 접촉원보다 큰 반지름을 가지면 1개보다 많은 교점을 가집니다. 따라서 $R\le \frac{1}{2a}$여야 합니다.

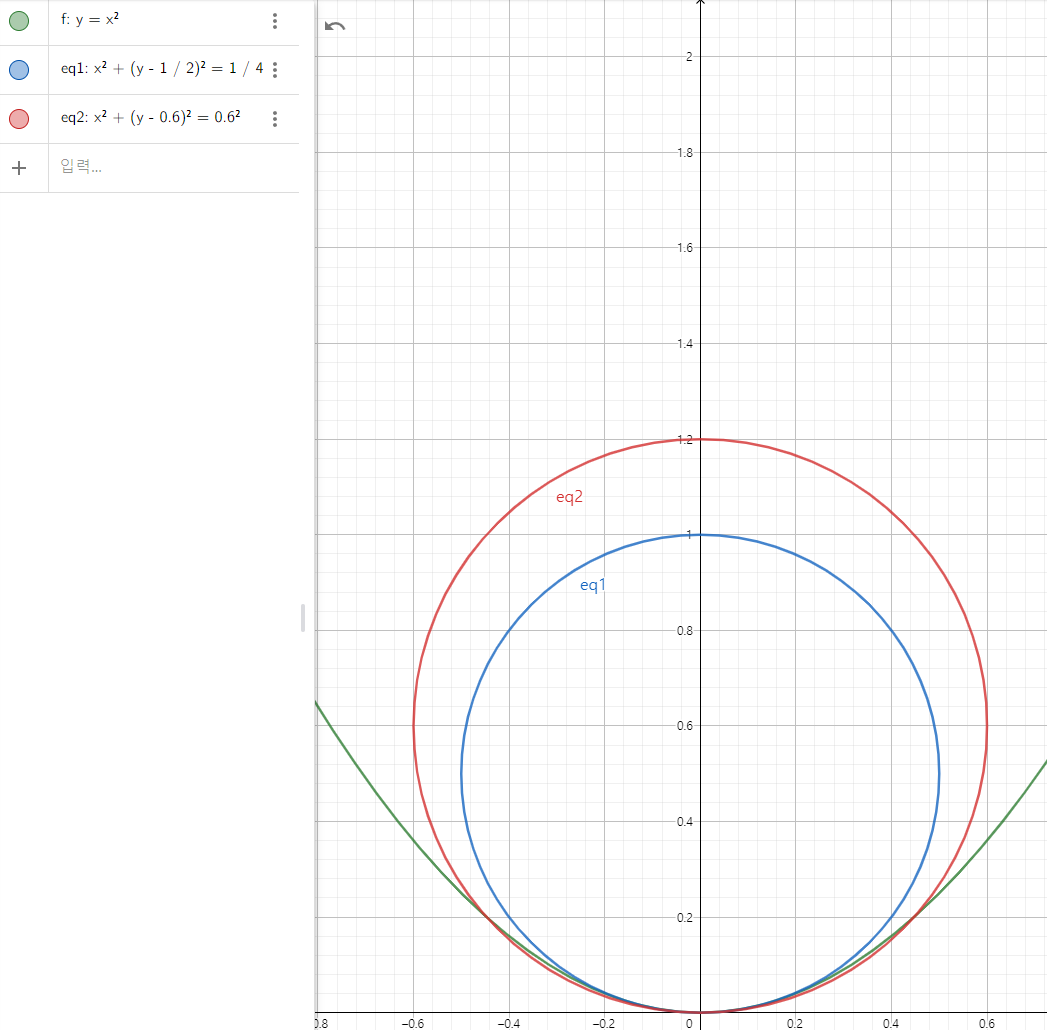
그래프를 그려봤을 때 실제로 $R=0.6>0.5$이면 교점이 3개 나옴을 확인할 수 있습니다.

참고

첫번째 그림은 마리온 솔루션, 2,3번째 그림은 수학이야기 블로그에서 따왔습니다.