f(f(x))=x의 해와 로지스틱 맵의 주기성
오늘이 역학 시험인데 역학 시험범위에 안 들어가지만 역학 책에 들어있는 카오스계에 대한 내용이 흥미로워서 읽다보니 고등학교 수준 칼럼으로 간단하게 써볼만해서 써봅니다.
왜 시험범위에 안 들어있는 걸 지금 읽고 있느냐 하면 공부하기 싫어서요..
$x_{n+1}=f(x_{n}), f(x)=ax(1-x)$라 하자. $a$는 $2$ 이상 $4$ 이하의 실수이다. ${x_n}$에 대해 유한한 개수의 초항 이후에 주기성($x_{n+N}=x_n$)이 나타날 경우 이를 수열의 주기라고 하자. 주기가 2가 되는 $a$들의 집합에 대해 이 집합의 하한은?
문제를 간단하게 요약해보면 위와 같습니다. 지금도 사실 대충 보기에 뭔가 간단해 보이지만 좀 더 다듬으면 논술이나 평가원 스타일로 굉장히 간단한 문제처럼 보이게 만들 수 있을 것 같습니다. 물론 보기에 간단한거지 깊게 파고 들어가면 생각처럼 간단한 문제는 아니지만 단순히 "주기가 2가 되는 a의 경계"(특히 하한)를 구하는 것은 어렵지 않습니다.
참고로 초항 x_1은 "잘" 골라야 합니다. (사실 주기의 정의는 저대로 하면 수학적으로 좀 문제의 소지가 있을듯하지만 ㅎㅎ; 물리학 책 에서 나온 내용이다보니 수학적으로 다듬기 쉽지 않은데, 혹시라도 덧붙이자면 표현에 너무 집착하지 마세요. 저도 큰 고민 없이 쓴 문 장입니다.)
아래는 해설입니다.
일단 여기서 f(x)=ax(1-x)는 로지스틱 맵이라 부릅니다. 맵은 잘 아는 map, 사상을 말하는데 쉽게 말하면 그냥 함수입니다.
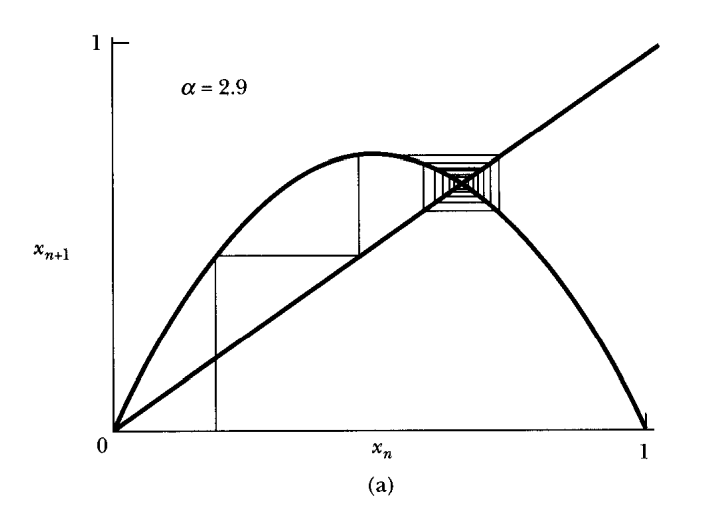
a=2.9일때 {x_n}은 위와 같이 한 점으로 수렴합니다. y=f(x)과 y=x를 그려놓고 y축에 평행하게 한번, x축에 평행하게 한번 번갈아가면서 이동하면 어디로 수렴하는지 알 수 있습니다. 고등학교 수학을 배운 분이라면 아마 어떻게 하는건지 알 겁니다.
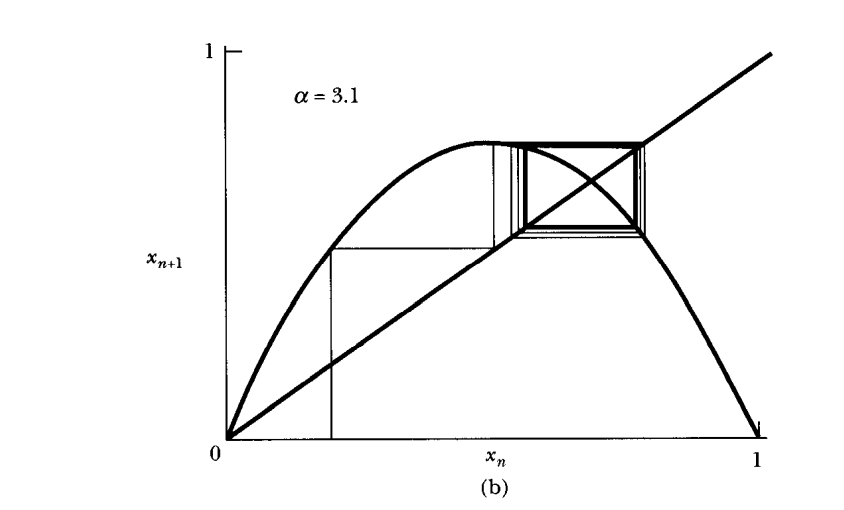
a=3.1일때 특정 초깃값에서 시작하면 2를 주기로 계속 사각형을 빙빙 돌게 됩니다. a=2.9일때와는 전혀 다른 결과입니다.
특히, a=3일때를 기점으로, a=3이거나 이것보다 조금 작으면 주기가 2가 아닌데(한 점 수렴) 3보다 조금이라도 크면 주기가 2가 됩니 다.
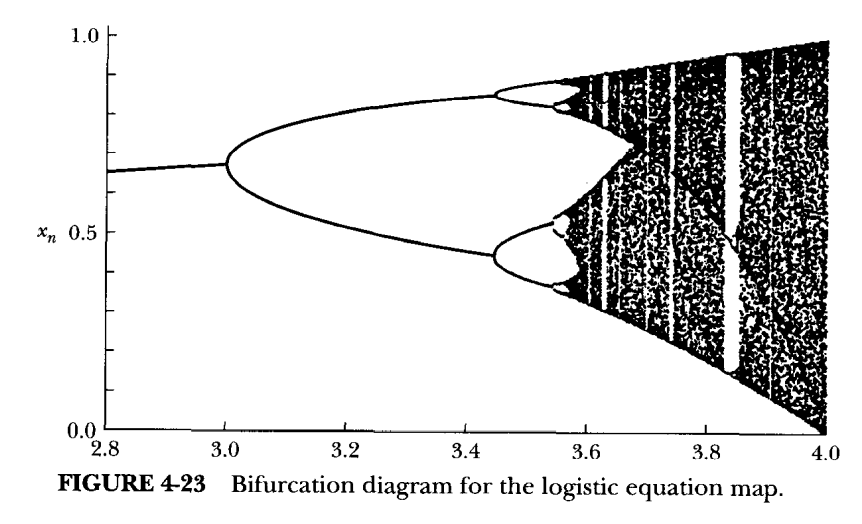
a에 따라(위 그래프의 가로축) 수렴하는 x값(세로축)을 나타내면 위와 같습니다. 꽤 신기한 모양이 나오고 특히 뒷부분에 대해서는 이론적으로 설명하는 바가 많지만 이 글에서는 간단히 왜 3.0에서 분기가 일어나는지만 설명하려고 합니다. 궁금한 사람은 https://horizon.kias.re.kr/20925/ 여기서 잘 설명하고 있으니 참고해 보세요.
주기가 2다, 라는 말을 다르게 해석하면 f(f(x))=x인 x가 존재한다는 말이 됩니다.
이러기 위해서는 y=f(f(x))를 그려놓았을 때 y=x와 교점이 존재하되, 그것이 0이나 x=f(x)의 해(이 경우는 주기가 1)가 아니어야 합니다.
f(f(x))=x의 교점? 이건 고등학교 사설문제 풀어본 사람이면 언제 이런지 다 알 겁니다.
-
x=f(x)
-
y=f(x)위의 두 점이, y=x에서 같은 거리에 떨어져 있고, 그 중점이 y=x 위에 있는 경우
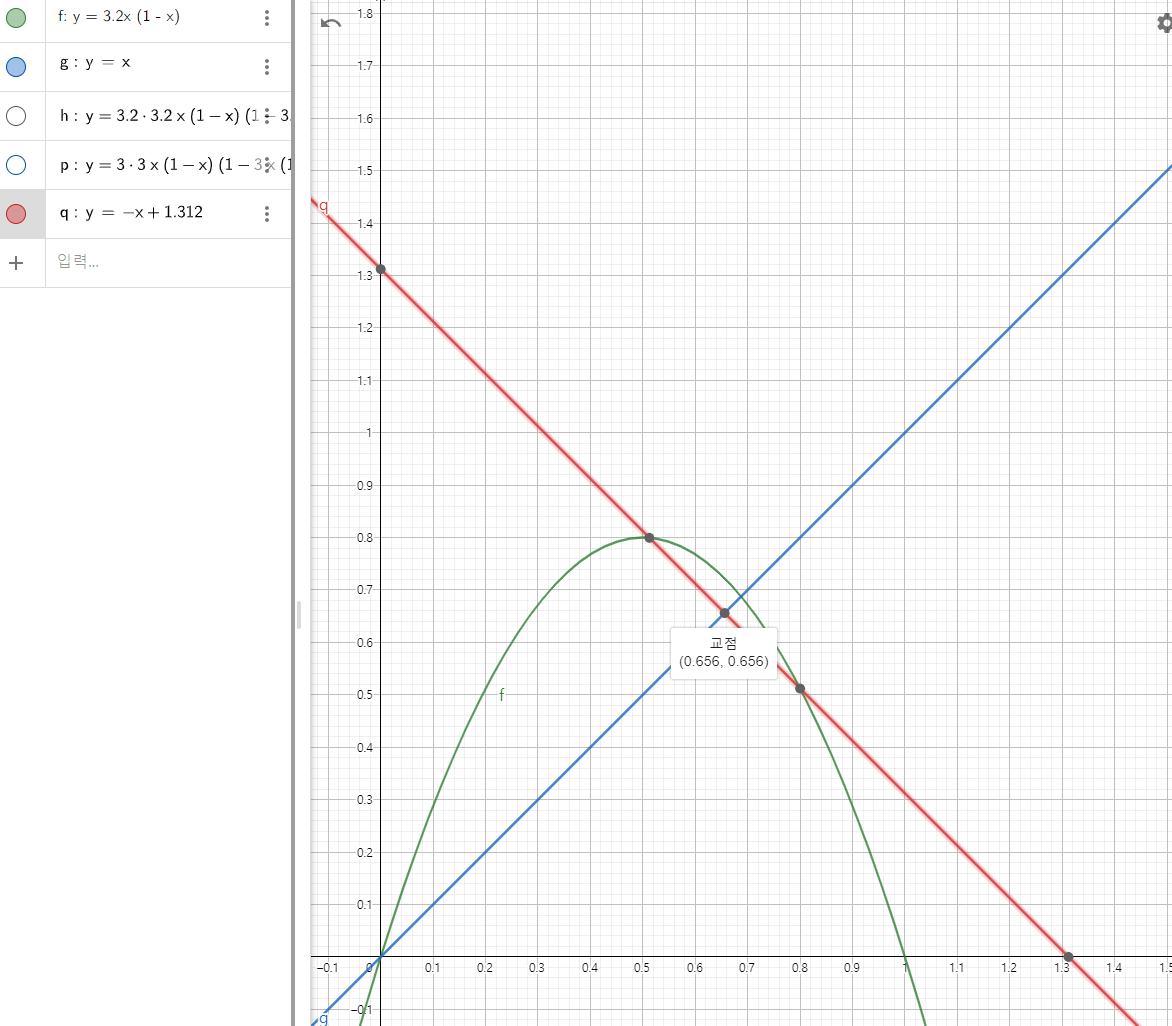
이를 고려해 대충 a=3.2에 대해 그래프를 그려보면 위와 같습니다. 특히 y=-x+1.312 정도를 그어보면 두 교점이 나오는데, 이 두 교점에서 y=x까지 거리는 같고 중점은 당연히 y=x위에 존재합니다.
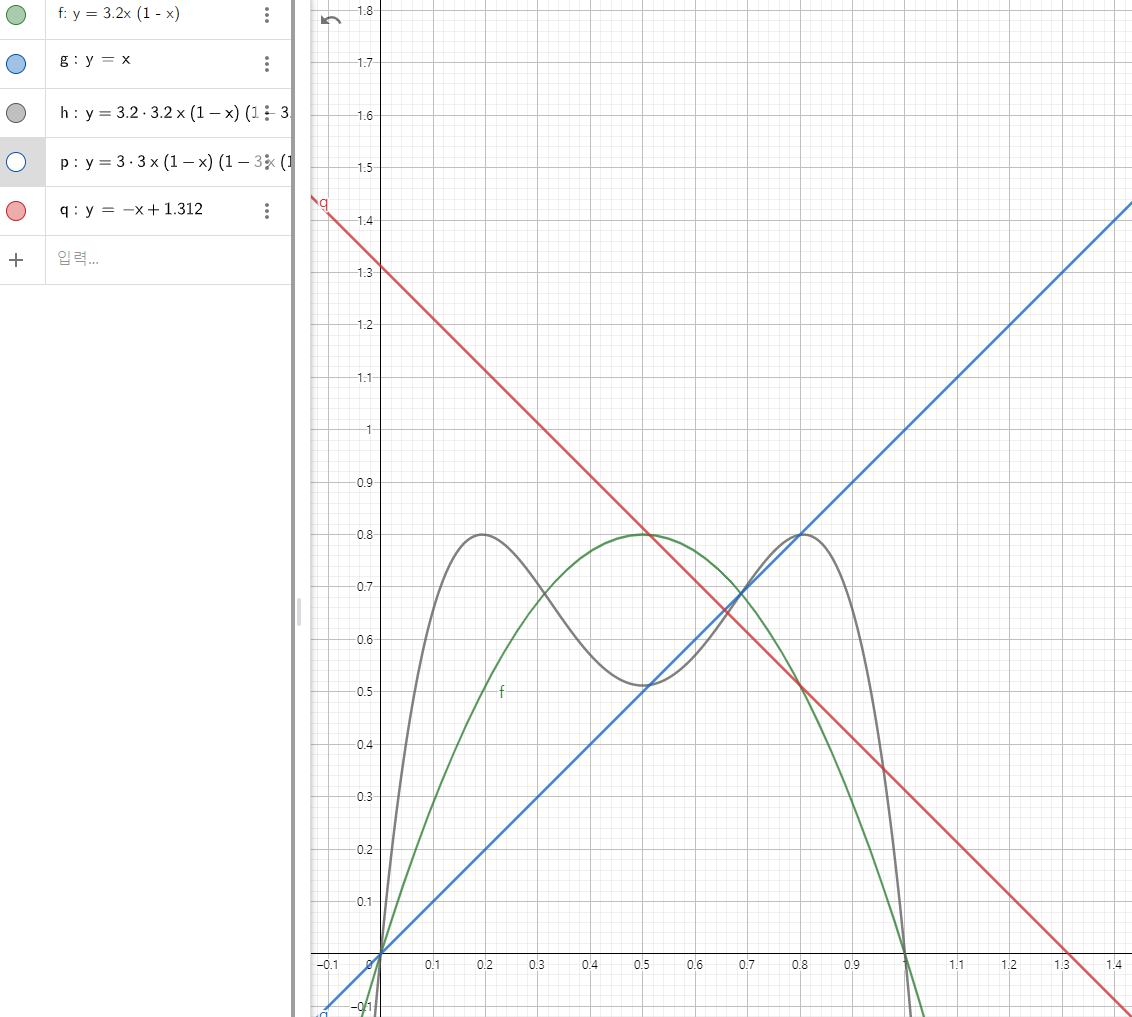
시험삼아 y=f(f(x))를 그려보면 위와 같이 나옵니다. x=f(f(x))의 해 위치에서 y=-x+1.312와 y=f(x) 교점의 x좌표가 나옴을 알 수 있습 니다.
이제 이러한 f(f(x))=x의 해가 존재하기 위한 조건을 생각해봅시다. 왠지 f(x)=x의 교점에서 f'(x)<-1이면 될 것 같습니다. 이를 수식으로 풀어보면 a>3이라는 게 쉽게 나옵니다. (유도는 전혀 어렵지 않으니 직접 해보셔도 어렵지 않을 겁니다)
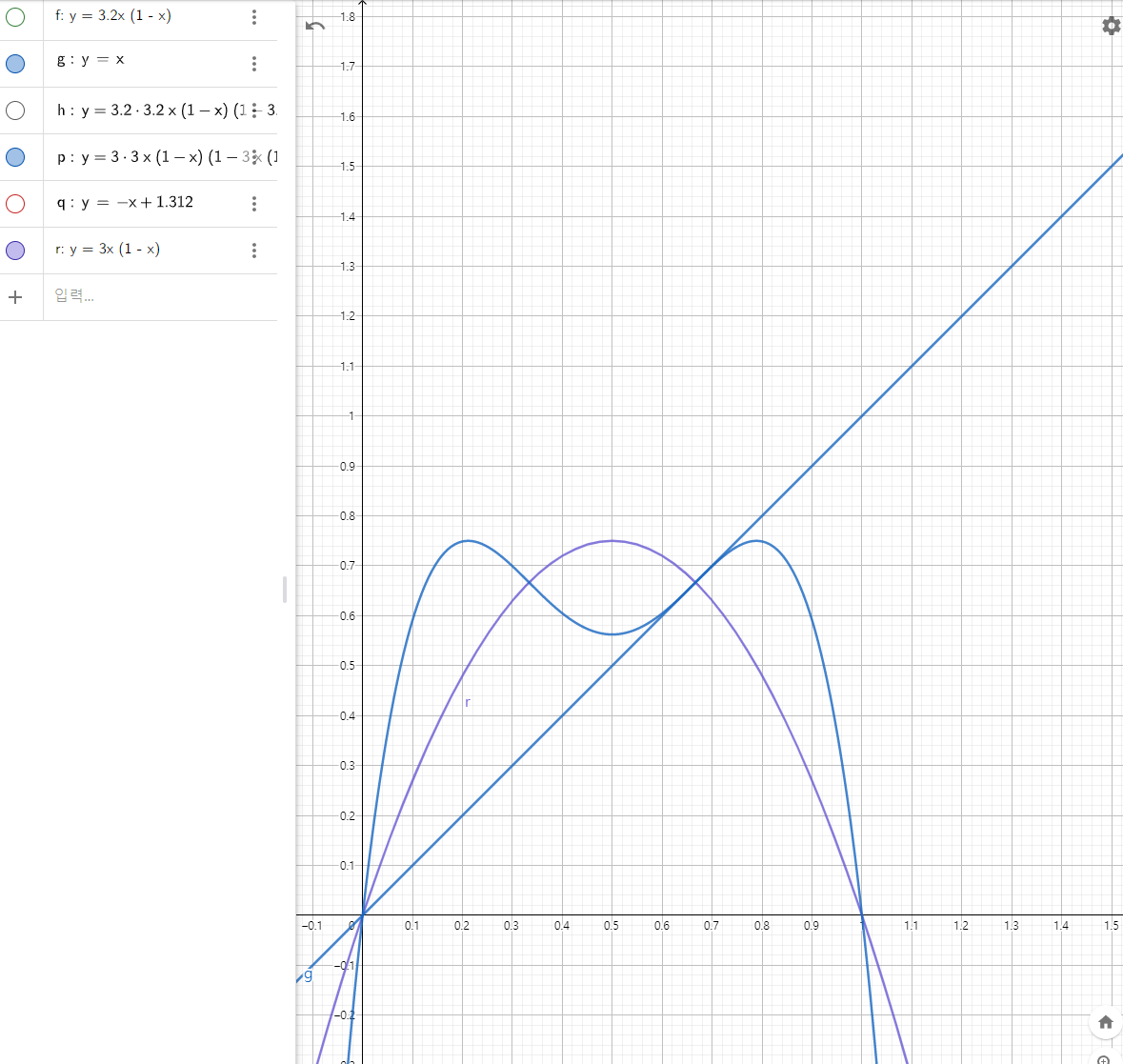
f(x)=3x(1-x)에 대해 y=f(f(x))와 y=x를 그려봤을 때 두 그래프가 예상대로 (y=f(x)와 y=x 교점을 제외했을 때) 두 개의 교점을 가지지 않고, (뚫)접하는 것을 확인할 수 있습니다.
geogebra로 간단히 그린 그래프 이외의 figure은 마리온 역학에서 따왔습니다.