190930나형 풀이

서론

내가 본 이 문제의 거의 대부분의 풀이가 대칭성과 관련된 오류, 논리적 비약을 범한다. 현장 풀이라면 대충 f(a)=a=1.5로 대칭적이지 않을까? 변곡점이 아닐까? 짐작하는 것은 나쁜 태도는 아니지만(실제로 ‘변곡점이지 않을까?’ 라는 짐작은 출제 포인트에 있어서도 꽤 가능성 있는 추측이다.), 기출문제를 제대로 자리에 앉아 분석하는 입장에서 이러한 논리적 비약은 피해야 한다.

일단 풀이에 들어가기에 앞서 하나를 분명히 해두려고 한다. 나는 현장에서 학생들이 이러한 풀이를 쓰면 안된다고 지적하고 있는 것이 아니다. 현장에서 문제를 풀어야 하는 학생이라면 논리적 비약을 해서 넘어갔더라도 함수가 주어진 조건을 모두 충족한다면 f(5)를 구해서 답으로 쓰면 그만이다. 아무리 중간 풀이 과정이 이상하더라도 문제에서 주어진 조건을 모두 충족하면 그게 답이다. (또한 x=a에서 변곡점을 가진다는 건 문제의 출제 의도를 생각해보면 어느 정도 합리적인 추측이다.) 다만 아까 말했듯, 집에서 기출문제를 분석하는 입장에서는 당연히 오류 없이 정확한 풀이를 공부해야 한다.

내가 지적하는 것은 문제의 풀이 방법을 서술한 강사나 블로그다. 정확하고 오류가 없는 풀이를 올려야 하는 강사들이나 선생님, 또는 인터넷의 문제풀이 글들이 마치 이게 정확한 풀이마냥 논리적 비약이 있는 풀이를 올려두고 있다. 그리고 그러한 오류 풀이를 올려두고 애들에게 가르치고, 조회수를 올리고 있을 것이다. 수식을 끄적거려 놓고서는 뒤쪽에 괄호를 열고 대칭성 때문라고 대충 한마디 던져두는 풀이가 너무나 많다. 대체 왜 대칭적이어야 하는지 이해가 가지 않는다. f'(0)-f'(1)=6 조건을 고려하기도 전에 대충 (1.5, 1.5)에 대칭적이다~라고 하고 넘어간다. f'(0)-f'(1)=6 조건이 없으면 대칭이 아니어도 되는데 말이다.

결론에서 한번 더 말하겠지만, 개인적으로는 이런 문제를 출제한 것도 바람직하지 않다고 생각하고 있다. 이렇게 대부분의 풀이에 논리적 비약이 포함되어 있는 것도 애초에 이런 문제를 출제한 것 때문이 아닌가 싶다.

풀이

f(f(x))=x의 해는 f(x)=x의 해이거나 f(p)=q, f(q)=p)를 만족하는 두 쌍이다.

i)번 케이스는 f(x) 개형을 생각하면 최소 1번 있다. ii)번 케이스는 짝수개 존재한다. 그런데 ii)번 케이스를 4번, i)번 케이스를 1번 만드는 것은 불가능하다. ii)번 케이스를 4번 만들면 i)번 케이스 개수가 1개보다 커진다.

비슷한 논리로 모든 경우를 고려하다보면 i)번 케이스를 3번, ii)번 케이스가 2번 나오는 경우를 f(f(x))=x의 해를 5개 만드는 적절한 경우라고 할 수 있다. f(1)=2, f(2)=1이 ii번 케이스고 i번 케이스로 f(0)=0, f(a)=a, f(b)=b가 나온다고 하면 문제 조건에 모순되지 않는다. (정확히 푸려면 다른 경우가 왜 안 되는지 논증해야 하나, 직접 강의로 설명하는 것도 아니고 블로그 줄글로 설명하려나 한계가 커서 설명은 생략한다.)

f(x)=ax^3+bx^2+cx+d, 또는 f(x)-(3-x)=a(x-1)(x-2)(x-b)꼴로 놓고(이 식에서 a,b는 문제에서 제시한 a,b와 다르다) f(0)=0, f(1)=2, f(2)=1, f'(0)-f'(1)=6을 모두 연립하면 미정계수가 4개이며 주어진 조건이 4개이므로 4원 연립방정식을 세워 문제를 풀 수 있다.

잘못된 풀이

f(0)=0, f(1)=2, f(2)=1 만족해야 한다는 것까지 관찰한 후 대충 그래프가 왜인지 (1.5, 1.5) 대칭일 것 같고 변곡점이 (1.5, 1.5)일 것 같은 기분이 드니 f(1.5)=1.5이며 f''(1.5)=0으로 두고 푸는 풀이가 있다. 말도 안되는 풀이이며, (1.5, 1.5)에 대칭적이라는 사실은 애초부터 모든 문제 조건을 고려해야 비로소 결과적으로 성립하는 사실이기 때문에 그러한 풀이는 논리적 비약을 갖고 있다.

반례로 내가 제시한 함수 $$f(x)=\frac{2}{3}x^3-\frac{7}{2}x^2+\frac{29}{6}x$$는 아래와 같은 개형으로, f(0)=0, f(1)=2, f(2)=1, f'(1)<0, f'(2)<0, f'(0)-f'(1)>0까지 만족한다. 유일하게 f'(0)-f'(1)=6은 만족하지 않는다. f'(0)-f'(1)=6까지 만족하게 만들면 정답인 함수로 함수가 확정되어 버리기에 조건을 f'(0)-f'(1)>0으로 약화시켰다.

보충 설명

내가 논리적 비약인 부분이 논리적 비약이라고 말하는 이유를 보충 설명하자면, 나는 f'(0)-f'(1)=6 조건을 고려하지도 않고 대충 대칭적이니까 f(a)=a=1.5이고, x=a에서 변곡점을 가지겠지? 라고 생각하는 그 사고를 논리적 비약이라고 말하는 것이다.

애초에 x=a에서 변곡점을 가지게 되는 건 f'(0)-f'(1)=6을 포함해 모든 문제의 조건을 빠짐없이 고려하게 되면 그때야 비로소 x=a에서 변곡점을 가지게 되는 것이다. 변곡점을 가진다고 먼저 확정지어버리고 f'(0)-f'(1)=6를 고려하는 풀이는 당연히 문제가 있다고밖에 생각할 수 없다. 나는 논리적 비약이 있는 풀이를 처음 들었을 때부터 분명 반례가 있을 것 같다는 생각이 들었는데, 왜 다들 그런 지적을 안 하는지 모르겠다.

실제로 f'(0)-f'(1)=6 조건 없이, x=a에서 변곡점을 가지지 않는 함수가 내가 제시한 반례이고. 그래프는 아래와 같이 나온다.

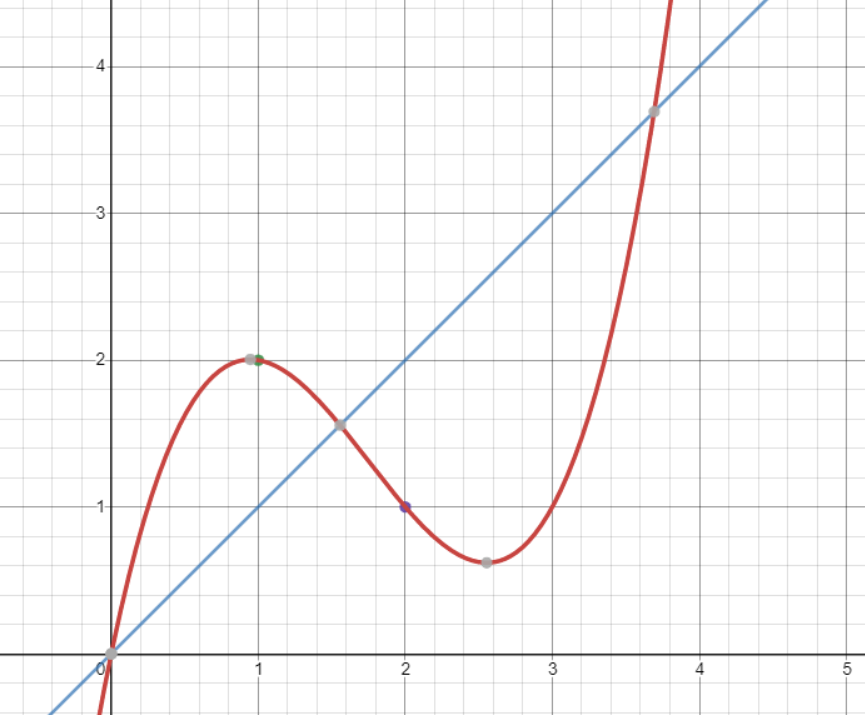
위와 같이 실제로 실근은 5개가 정상적으로 나온다.

결론

나는 개인적으로 이 문제가 상당히 좋지 않은 문제라고 생각한다. 먼저 논리적 비약을 통해 대충 대칭적이겠지~라고 생각한 학생은 상당한 어드밴티지를 얻고 문제를 풀 수 있으며, 실제로 ’정해’를 통해 문제를 풀려면 그냥 미정계수 설정하고 연립방정식 푸는 계산 노가다를 해야 한다.

풀이 하나는 논리적 비약이고 풀이 하나는 그냥 노가다라니, 사고력을 시험하는 수능 수학 시험의 취지에는 맞지 않는 문제라고 생각한다. 물론 이 정도 수준의 노가다는 별로 복잡할 것은 없으나 논리적 비약이 들어간 풀이를 구현한 학생이 어드밴티지를 얻는다는 것은 바람직하지 않다. 수능이 아닌 9월 평가원 모의고사라 이런 문제가 나올 수 있었다고 생각한다.

2021-08-21 수정

오늘 다시 찾아보니 제대로 된 풀이를 올린 영상들이 꽤 많이 보인다. 잘못된 풀이에 대해서도 내가 설명한 것과 똑같이 지적하고 있는데 굉장히 바람직하다고 생각한다.