파생금융상품(Derivatives) 1
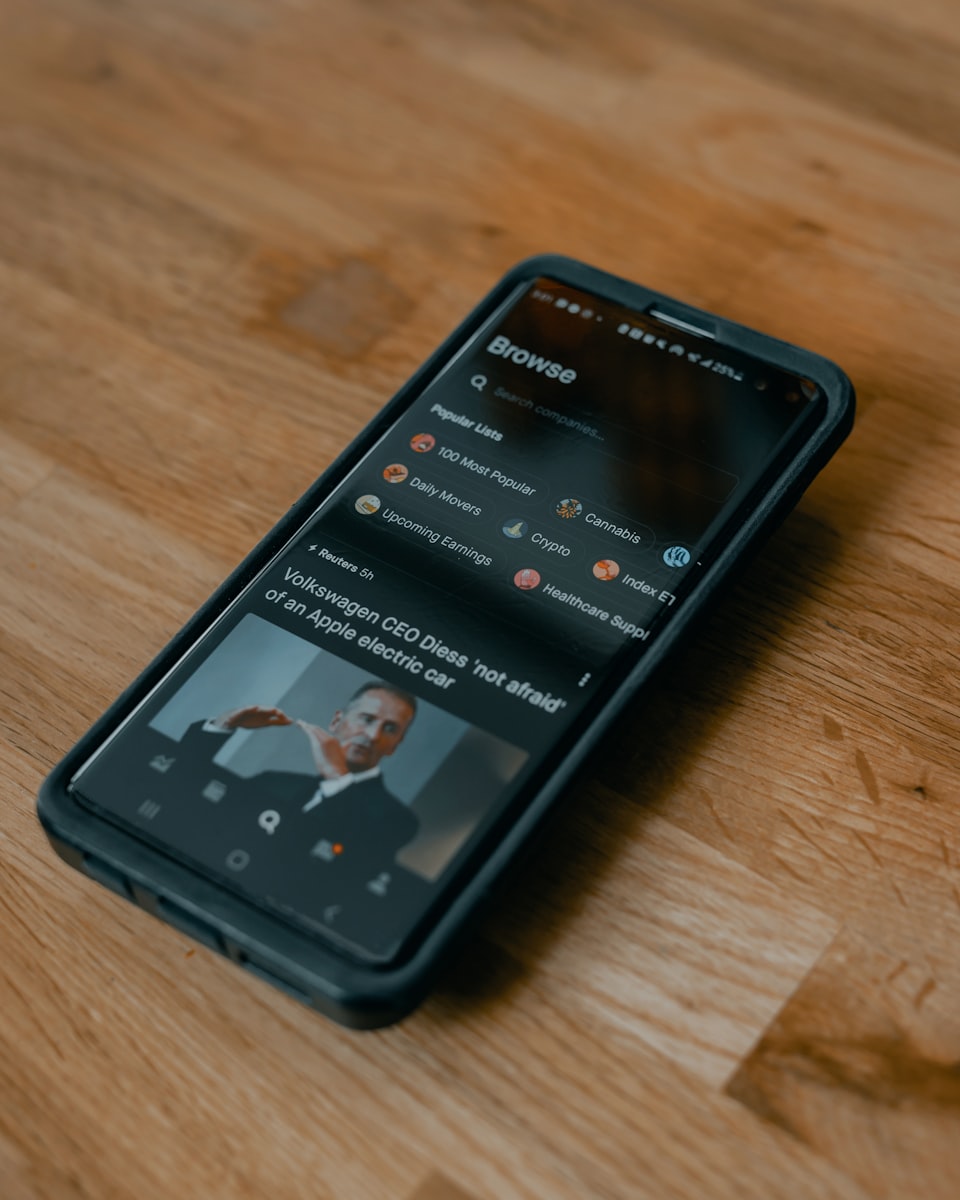
파생금융상품(Derivatives)
- 파생금융상품이란, 기초변수에 의해 가치가 결정되는 금융상품을 이른다. 여기에서 기초변수란 금리, 상품의 가격, 날씨, 전기 등 다양하게 나타날 수 있다.
- 계약 형태에 따라 선물, 옵션, 스왑 등을 한다.
- 주가지수, 주식 선물 등은 장내 거래(거래소, 표준화된 계약)
- 금리, 통화 파생상품들은 대부분 장외 거래(당사자간 거래, 브로커 중개)
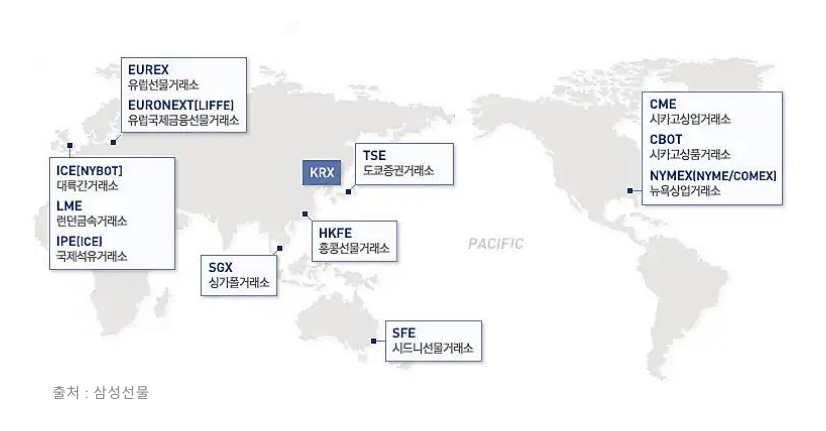
파생금융상품에는 나타나는 여러 특성은 아래와 같다.
- zero net supply
- 수요에 따라 공급이 나타나므로 net supply가 0이 된다.
- market paritipants: hedgers, speculators, arbitragers
- hedging
- 헷징(손실을 막기 위한 대비)로 자주 사용된다.
- Leverage
- 크게는 100배 이상까지, 큰 레버리지를 가용한 거래가 많이 나타난다.
- 'Wag the dog'
- 파생상품의 가격이 오히려 기초변수의 변화를 창출하는 현상을 wag the dog, 개의 꼬리가 개를 조종하는 것이라 이른다.
선도계약(Forward Contract)
특정 상품(기초자산, underlying asset)을 현재 시점에서 합의한 가격(선도가격)으로 미래의 특정 시점(만기일)에 인도할 것을 약정하는 두 당사자간의 계약
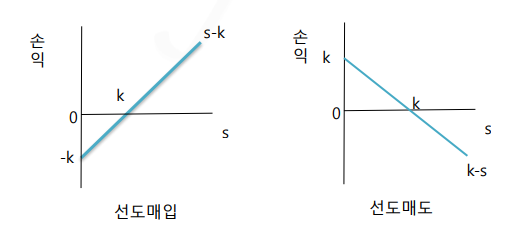
- 만기일에 선도계약 매수자는
현물가격-선도가격만큼 이득 또는 손해, 매도자는선도가격-현물가격만큼 이득 또는 손해가 발생한다.
선물(Futures)
선도계약과 유사하나, 차이점은 거래소 상장 여부이다.
- 선도 계약과 달리 모든 조건이 표준화
- 거래소에서 수시 거래
- 매일 손익 정산(mark-to-market)
- 매일 증거금 체크
- 상품선물(농산물, 축산물, 임산물, 광산물, ...)
- 금융선물(통화, 금리, 개별주식, 인덱스, ...)
- 상품의 실제 인수도가 이루어지는 경우는 드물다고 한다. (ex. 원유 선물)
증거금 제도
- 계약불이행을 막기 위해 요구하는 최소한의 금액
- 개시증거금(initial margin), 유지증거금(maintenance margin)
- margin call과 강제 포지션 청산
- 증거금이 부족할 경우 margin call이 발생하고, 마진 요구를 만족하지 못하면 강제 청산이 발생한다.
선물의 이론가
파생상품은 이론적으로 무위험자산과 기초자산의 조합으로 복제할 수 있다.
ex) 만기가 3개월인 주식 선물의 경우,
3개월 뒤 선물가격을 지불하고 주식 보유 = 3개월동안 현재가를 대출받아 주식을 보유
따라서 선물가 = 현재가 + 이자이고, 수식으로 나타내면 $F=Se^{rT}$와 같다.
쉽고 간단하게 말해, 만기 시점에 예상되는 자산의 가격이 선물의 이론가가 된다.
옵션(Option)
선도 계약과 유사하나, '강제성'을 띄지 않는다.
콜 옵션(call option)
만기 시점(expiration date)에 옵션 발행자(seller or writer)로부터 행사가(strike price)로 기초자산(underlying asset)을 살 수 있는 권리가 주어지는 파생상품
call option의 매수자는 만기 시점에 행사가로 기초자산을 팔 수 있는 '권리'에 대해 수수료를 매도자에게 지급한다. (initial cost)
콜 옵션의 매수자
행사가 50, 가격이 1.5인 콜 옵션의 매수자의 payoff를 그래프로 나타내면 아래와 같다.
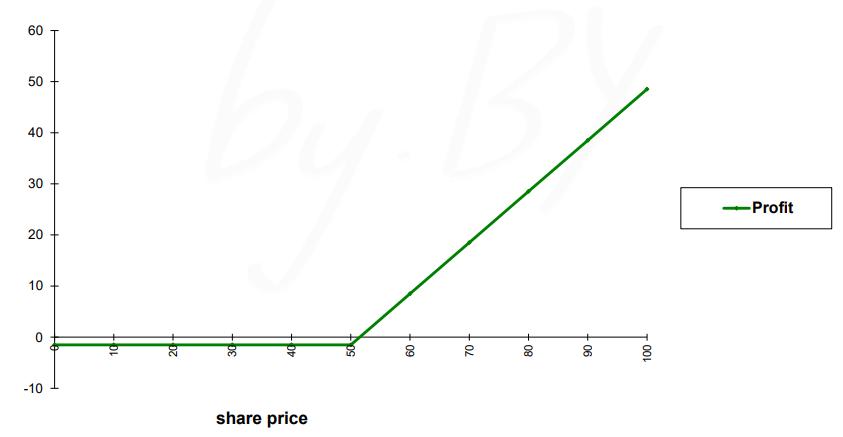
그래프를 해석하자면, 기초자산의 가격이 50을 넘어가기 전까지는 수수료 -1.5로 profit이 일정하다. 기초자산의 가격이 50이 된 후부터 기초자산의 가격에 정비례해 profit이 선형적으로 증가하며, 기초자산의 가격이 51.5가 될 때 profit=0이 된다.
수식으로 나타내면 $y=max(x - 50, 0) - 1.5$로, DNN에서 자주 사용하는 ReLU의 꼴이 된다.
콜 옵션의 매도자
매도자는 매수자와 정확히 반대, -1을 곱한 꼴의 payoff를 가진다.
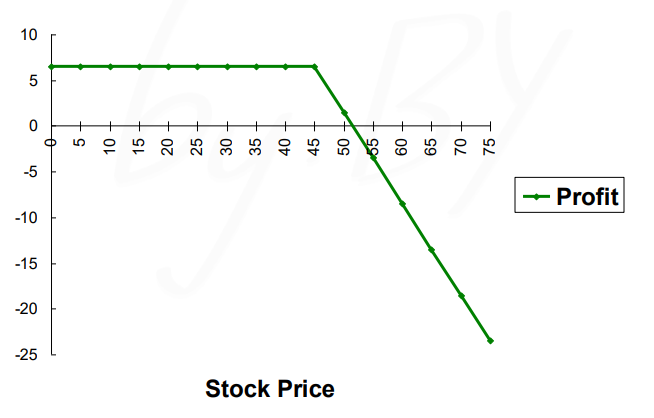
풋 옵션(put option)
만기(expiration date)시점에 옵션 발행자(seller or writer)에게 행사가(strike price)로 기초자산(underlying asset)을 팔 수 있는 권리가 주어지는 파생상품
- Exercise styles
- European: 옵션이 오직 만기에만 행사 가능
- American: 옵션이 어느때나 행사 가능
- Bermudan: 옵션이 미리 정의된 어떠한 시점들에 행사 가능
마찬가지로 옵션의 매수자가 매도자에게 팔 수 있는 권리에 대한 수수료를 지급한다.
풋 옵션의 매수자
행사가 15, 가격이 3인 풋옵션의 매수자의 payoff는 아래와 같다.
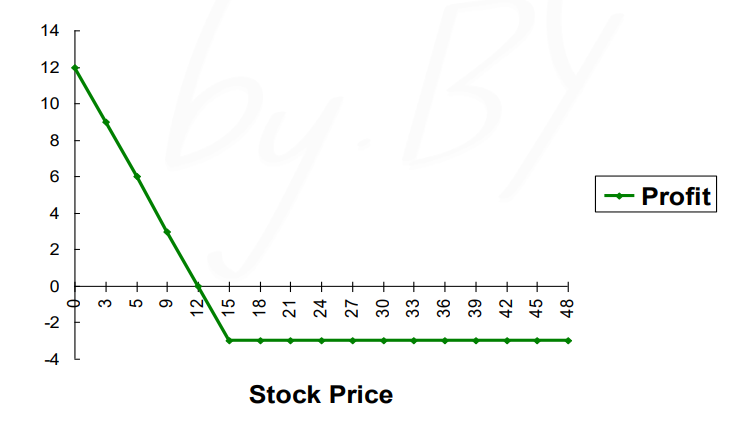
기초자산의 가격이 떨어졌을 때, 이전의 비싼 가격에 팔 수 있다는 장점이 있으므로 기초자산의 가격이 떨어질 때 유리하다. 이를 이용해 풋 옵션과 Long을 조합해 hedging 전략을 구성하기도 한다.
Option pricing
call option의 매수자 기준으로, 기초자산의 가격이 오르면 기존의 싼 가격에 살 수 있으므로 유리하고, put option의 매수자 기준으로는 기초자산의 가격이 오르면 손해다.
call option이든 put option이든 기초자산의 volatility(유동성)이 클수록 유리하고, 통상적으로 만기까지의 시간이 길수록 기초자산의 가격이 바뀔 확률이 높으므로 만기까지의 시간이 길수록 유리하다.
기초자산의 현재가격을 기준으로 행사가가격의 위치에 따라 내가격(ITM), 등가격(ATM), 외가격(OTM) 옵션으로 구분하기도 한다.
예를 들어 콜옵션 기준으로, (K는 행사가, S는 현재 시점에 기초자산의 가격)
- K > S: 외가격 옵션, 내재가치 = $max(0, S - K) = 0$
- K = S: 등가격 옵션, 내재가치 = $max(0, S - K) = 0$
- K < S: 내가격 옵션, 내재가치 = $max(0, S - K) > 0$
즉 내가격 옵션(ITM)이 가장 가치가 높다.
Put-Call Parity
선물에서와 마찬가지로 콜옵션을 다른 자산을 이용해 복제하는 것이 가능하다.
- European Call + $Ke^{-rT}$ risk-free asset
- European put + one underlying asset
만기 시점의 가격이 S*, 행사가가 K면,
1번 시나리오의 경우 S*>K면 (S*-K)+K=S*의 이득, S*<K면 K의 이득을 얻는다.
2번 시나리오의 경우 S*<K면 K의 이득, S*>K면 S*의 이득을 얻는다.
두 시나리오는 똑같은 결과를 유도하며, 따라서 $C+Ke^{-rT}=P+S$가 성립한다.