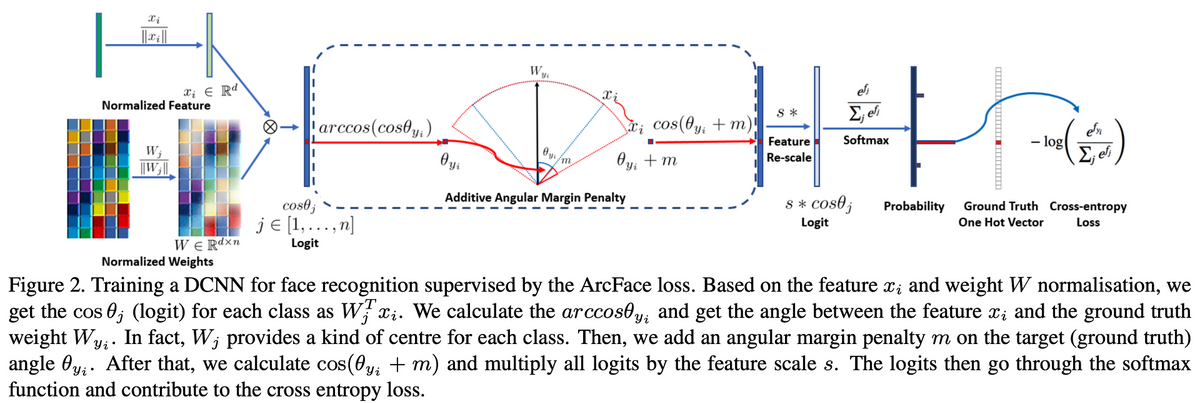
ArcfaceLoss는 간단히 말하면 Softmax+Cross Entropy Loss(CE Loss)를 개량한 것이라 보면 된다. 관련 논문은 arXiv 기준 2018년에 처음 Submit되었다. 사용법이 매우 간단하고 동시에 성능은 상당히 좋다.

용어 정리

• Logits: softmax 직전 레이어의 출력값

Softmax+CE Loss

ArcfaceLoss에 대해 알아보기 전에, 가장 고전적(?)으로 쓰이는 Softmax+CE Loss에 대해 먼저 알아봐야 한다.

알다시피 Softmax 함수는 아래와 같이 작동한다.
$$\dfrac{e^{W^Tx+b}}{\sum e^{W^Tx+b}}$$
distribution p에 대한 distribution q의 Cross Entropy는 아래와 같다.
$$H(p,q)=-E_p[\log q]$$
분류 문제에서 목표 distribution p는 One-Hot Encoding을 따라 만약 정답 레이블이 $y_i$라면 $y_i$번째 원소만 1인 벡터일 것이다. 따라서 CE Loss는 아래와 같이 정리된다.
$$\mathcal{L}_{CE}=-\log{q_{y_i}}$$
$N$개의 학습 데이터를 일괄적으로 처리할 때 Loss는

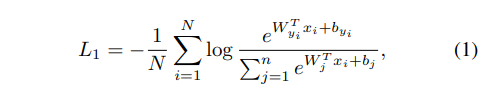
ArcfaceLoss의 선행 논문으로 SphereFace(Liu et al, 2017)가 있다. 구체적인 배경이 필요한 사람은 읽어보자. 나는 소스코드 분석 및 활용 위주로 글을 서술할 예정이기에 관련 내용은 생략한다.

ArcfaceLoss

CE Loss는 아래와 같이 변형할 수 있다. $W$와 $x$의 내적은 결국 $|W||x|\cos\theta$로 바꿀 수 있기 때문이다.

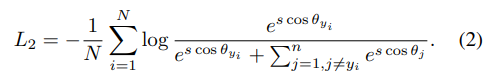
결국 $W$, $x$를 정규화시켰을 때 필요한 인자는 $\theta$ 하나가 되고, 분류 문제가 hypersphere mapping 문제로 변한다. 각 클래스에 대응되는 학습 데이터가 hypersphere 위의 점들에 대응되며, hypersphere 위에서 경계를 어떻게 나누느냐에 따라 NN의 성능이 바뀐다는 것이다. 또한 NN의 마지막 Fully-Connected Layer의 Weight Matrix의 column(convention에 따라 row가 될 수도 있겠다)이 각 class의 central representation이 된다.

ArcfaceLoss는 굉장히 간단하다. 정답 레이블의 각도 $\theta_{y_i}$에 angular margin penalty $m$만 더하면 된다.

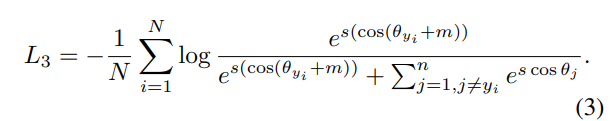
놀랍게도 이게 끝이다. 도대체 이렇게 $m$을 더해준 게 어떤 영향이 있는지 시각적으로 확인하면(toy example) 아래와 같다. angular margin penalty에 의해 여러 class가 hypersphere 위에서 더 명확하게 구분된다.

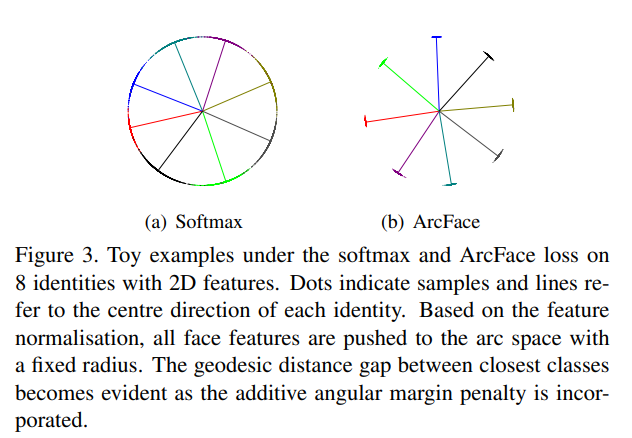
논문 안에는 아래와 같은 그림이 있는데 arccos 연산은 불필요하다. 어차피 코사인 덧셈법칙으로 $\cos(\theta+m)$이 전개 가능하기 때문이다. 자세한 내용은 후술할 실제 구현을 참고하라.

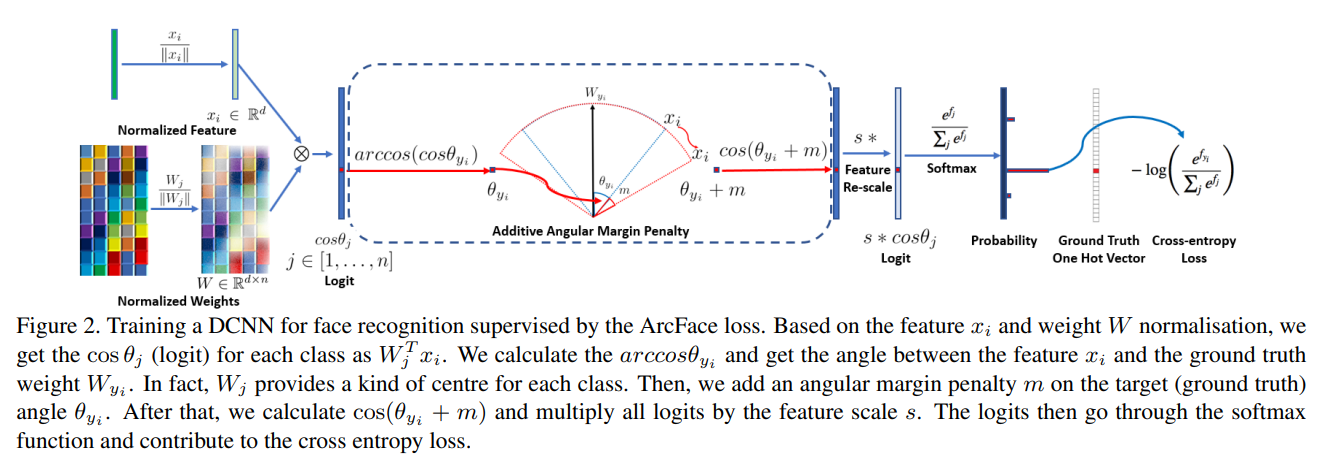
ArcMarginProduct_subcenter

ArcfaceLoss의 간단한 개량형이다.

https://www.kaggle.com/c/landmark-recognition-2020/discussion/187757
여기에서 ## architecture: sub-center ArcFace with dynamic margins 섹션을 보면 설명이 잘 나와있는데, 한글로 옮기면 그냥 하나의 class가 hypersphere 위에서 여러 center을 가질 수 있기에 그걸 고려했다는 말이다.

ArcFaceLossAdaptiveMargin

ArcFaceLoss을 더더욱 개량한 형태이다.

https://www.kaggle.com/c/landmark-recognition-2020/discussion/187757
여기에서 ## architecture: sub-center ArcFace with dynamic margins 섹션의 끝부분을 보면 나와 있는데, GLD dataset(Googld Landmark Recognition에 쓰이는 dataset이다)는 long tails를 가지도록 매우 불균형 되어있다고 한다. 이를 해소하기 위해 smaller class에 더 큰 margin을 배치해야 했었고 그를 위해 Adaptive Margin, 즉 class의 크기에 의존해 변하는 margin을 설계했다고 한다.

소스코드 및 Competition 활용

https://www.kaggle.com/c/landmark-recognition-2020/discussion/187757
https://github.com/haqishen/Google-Landmark-Recognition-2020-3rd-Place-Solution
가장 활용하기 좋은 예시는 위에서 참고할 수 있다. ArcfaceLoss subcenter, ArcfaceLossAdaptiveMargin 모두 models.py에서 가져다 그대로 쓰면 된다. repository 저자의 경우 ArcfaceLoss를 적용하기 전 Swish 활성화 함수를 먼저 썼는데, 특별한 이유가 있는지는 잘 모르겠다. 궁금하네.

CE Loss에 smoothing을 구현한 것도 있는데 이거.. 지금 토치 CE Loss 문서 보면 label smoothing이 있는데 아마 이 때는 이게 없었거나 뭐가 활용하기에 문제가 있었거나 했던 게 아닐까 싶다.

https://github.com/ChristofHenkel/kaggle-landmark-2021-1st-place
이 사람도 2020 3rd의 솔루션을 빌려다 썼기에 ArcFaceLossAdaptiveMargin을 소스코드에서 확인할 수 있다.

가장 수정이 많이 이루어진 건 ArcFaceLossAdaptiveMargin이지만, ArcFaceLoss+subcenter만 가지고도 데이터 불균형이 없을 때는 ArcFaceLossAdaptiveMargin과 큰 차이가 없는 것 같았다. 1번 비교 실험해본 결과이므로 확실한 결과는 아니다.

또한 ArcFaceLoss를 사용할 경우 s와 m, ArcFaceLossAdaptiveMargin을 사용할 경우 s를 잘 조절해 줘야 한다. AdaptiveMargin을 사용했을 때 데이터셋, 모델 특성에 따라 최적의 $s$가 바뀌는 것을 확인했다. (CLOVA AIRUSH R1에서 pit_xs_224를 사용했을 때 s=20, rexnet_150을 사용했을 때 s=30이 최적이었다.)

소스코드 분석

class Swish(torch.autograd.Function):

    @staticmethod
    def forward(ctx, i):
        result = i * torch.sigmoid(i)
        ctx.save_for_backward(i)
        return result

    @staticmethod
    def backward(ctx, grad_output):
        i = ctx.saved_variables[0]
        sigmoid_i = torch.sigmoid(i)
        return grad_output * (sigmoid_i * (1 + i * (1 - sigmoid_i)))


class Swish_module(nn.Module):
    def forward(self, x):
        return Swish.apply(x)

먼저 Swish module인데... 도대체 왜 아래와 같이 구현하지 않았나 찾아보니 메모리를 덜 쓴다고 한다. 아니 근데 그 이유가 궁금한데 어디도 설명을 해주질 않네.. 짐작하기로 sigmoid의 미분은 sigmoid(x)(1-sigmoid(x)) 꼴이라 pytorch의 자동 미분 과정에서 x뿐만 아니라 sigmoid(x)가 저장되어 그런 것 같긴 하다. 정확한 이유는 모르겠다.

class Swish(nn.Module):
    def forward(self, input_tensor):
        return input_tensor * torch.sigmoid(input_tensor)

class ArcMarginProduct_subcenter(nn.Module):
    def __init__(self, in_features, out_features, k=3):
        super().__init__()
        self.weight = nn.Parameter(torch.FloatTensor(out_features*k, in_features))
        self.reset_parameters()
        self.k = k
        self.out_features = out_features

    def reset_parameters(self):
        stdv = 1. / math.sqrt(self.weight.size(1))
        self.weight.data.uniform_(-stdv, stdv)

    def forward(self, features):
        cosine_all = F.linear(F.normalize(features), F.normalize(self.weight))
        cosine_all = cosine_all.view(-1, self.out_features, self.k)
        cosine, _ = torch.max(cosine_all, dim=2)
        return cosine

보니 k=3이 class의 center 개수를 나타낸 듯 하다. 각각의 class에 대해 가장 가까운(코사인 값이 큰) center을 찾아 해당하는 코사인 값을 리턴한다.

class ArcFaceLossAdaptiveMargin(nn.modules.Module):
    def __init__(self, margins, s=30.0):
        super().__init__()
        self.crit = DenseCrossEntropy()
        self.s = s
        self.margins = margins

    def forward(self, logits, labels, out_dim):
        ms = []
        ms = self.margins[labels.cpu().numpy()]
        cos_m = torch.from_numpy(np.cos(ms)).float().cuda()
        sin_m = torch.from_numpy(np.sin(ms)).float().cuda()
        th = torch.from_numpy(np.cos(math.pi - ms)).float().cuda()
        mm = torch.from_numpy(np.sin(math.pi - ms) * ms).float().cuda()
        labels = F.one_hot(labels, out_dim).float()
        logits = logits.float()
        cosine = logits
        sine = torch.sqrt(1.0 - torch.pow(cosine, 2))
        phi = cosine * cos_m.view(-1,1) - sine * sin_m.view(-1,1)
        phi = torch.where(cosine > th.view(-1,1), phi, cosine - mm.view(-1,1))
        output = (labels * phi) + ((1.0 - labels) * cosine)
        output *= self.s
        loss = self.crit(output, labels)
        return loss

ArcFaceLossAdaptiveMargin의 경우 initializing 과정에서 margins를 입력해줘야 한다. 이는 각 class에 대응하는 margins로, 아래와 같은 방식으로 dataset 준비 과정에서 계산해 줘야 한다.

    # get adaptive margin
    tmp = np.sqrt(1 / np.sqrt(df['landmark_id'].value_counts().sort_index().values))
    margins = (tmp - tmp.min()) / (tmp.max() - tmp.min()) * 0.45 + 0.05
    def criterion(logits_m, target):
        arc = ArcFaceLossAdaptiveMargin(margins=margins, s=config.arc_s)
        loss_m = arc(logits_m, target, out_dim)
        return loss_m

Kaggle류의 Competition에서 활용하기 좋은 또 다른 종류의 loss로는 focal loss(Lin et al, 2017) 가 있다고 들었는데, 이게 가장 좋은 건지는 모르겠다. arcfaceloss랑 적절히 합칠 수도 있을 듯한데 이미 arcface에는 AdaptiveMargin이 고안되어 있으니 성격이 겹치기도 하네..

Reference

https://butter-shower.tistory.com/237
https://velog.io/@gtpgg1013/논문리뷰-ArcFace-Additive-Angular-Margin-Loss-for-Deep-Face-Recognition
https://aimaster.tistory.com/93