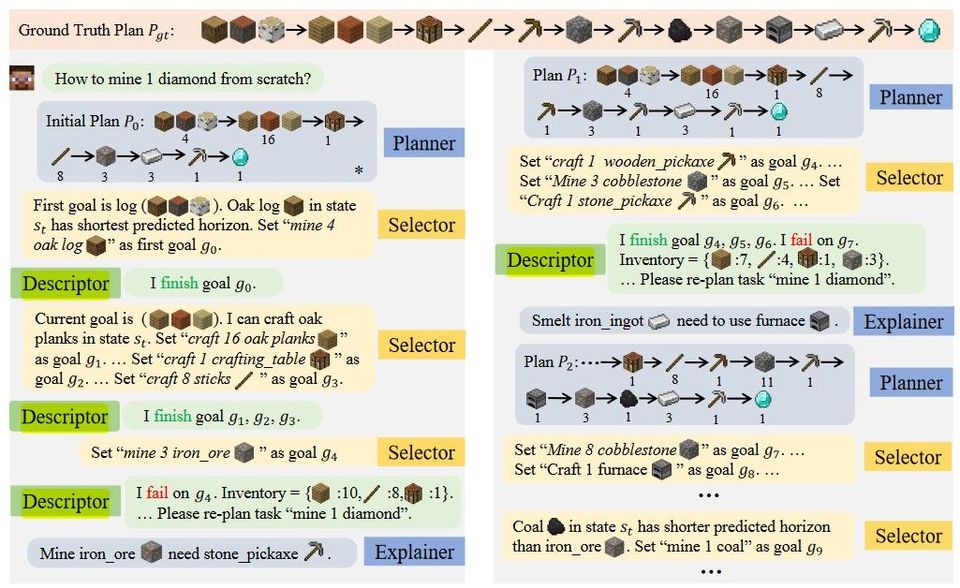
Fourier Neural Operator for Parametric Partial Differential Equations (ICLR 2021)
이 글은 논문의 모든 내용을 꼼꼼히 다루기보다는 핵심 내용만을 읽는데에 중점을 둡니다.
리뷰 논문은 Fourier Neural Operator, https://arxiv.org/abs/2010.08895 입니다.
Neural Operator
FNO(Fourier Neural Operator)에 대해 설명하기 전 neural operator에 대해 먼저 설명해야 한다. 기존의 ML은 finite dimensional Euclidean space나 finite set을 입/출력으로 삼았다. 함수를 입출력으로 하고 싶을 때 기존의 ML을 적용하는 간단한 방식은, 적당히 함수에 discretization을 적용하여 입/출력으로 때려넣는 방법이 있다. 하지만 이렇게 하면 discretization 방식을 다르게 해 resolution이 달라지면 모델을 아예 다시 훈련해야 하는 한계가 있다.
Neural operator은 무한차원 함수공간을 입출력으로 디자인된 인공신경망으로, discretization/resolution에 영향을 받지 않는다는 장점이 있다. (한번 훈련시킨 후에는 resolution이 달라져도 다시 훈련할 필요가 없다.) 물론 실제로는 sampling frequency에 따라 nyquist frequency가 달라지는 등 이슈가 있으나 일단 저자의 주장은 그렇다는 것이다. 아예 틀린 말도 아니기도 하고..
neural operator에 대해서는 https://zongyi-li.github.io/neural-operator/ 에서 잘 설명하고 있으며 자료도 잘 모여 있고, Neural Operator[1] 에서 neural operator 내용을 총망라해서 정리해두고 있으니 참고하면 도움이 될 것이다. 근데 참고하라고 제시한 논문은 FNO를 포함해 neural operator 내용을 전부 다 담아둔 거라 지금 보니 80페이지가 넘더라..
요약하면, neural operator은 bounded domain에서 함수공간 사이의 mapping 역할을 하며, 이 때 인공신경망을 이용한다. 참고로 Neural Operator[1:1]에서는 neural operator을 linear integral operator과 non-linear activation function의 합성으로 formulate했고, 이건 FNO에도 똑같이 쓰이는 중요한 내용이기에 기억해 둬야 한다.
그래서 무슨 쓸모가 있는가?
그래서 도대체 무한차원 함수공간 사이 매핑을 인공신경망으로 근사하는 게 무슨 쓸모가 있는가?(참고로 Neural Operator[1:2]에서, neural operator의 universal approximation theorem을 증명했다고 한다. 증명을 직접 읽어보진 않았다.)
대표적인 쓰임새가 바로 solving PDE이다. PDE를 풀기 위해서는 초기 조건 $u_0(x)=u(x, 0)$이나 coefficient function이 주어졌을 때 $u(x, t)$ 등을 구해야 한다. 다시 말해 함수가 입력이고 함수가 출력인 구조인데, neural operator로 이들을 풀 수 있다.
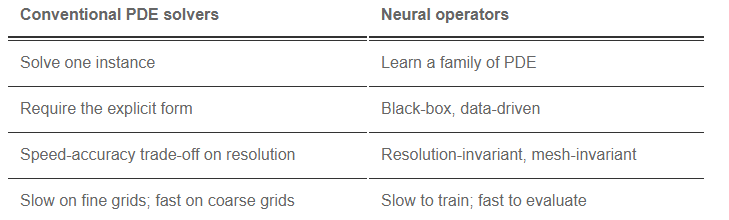
그럼 conventional PDE solver과 비교했을 때 neural operator가 어떤 장단점이 있는가? 위의 표를 블로그에서 제시하니 참고하면 좋을 듯하다.
Fourier Neural Operator
Fourier Neural Operator, FNO를 간단히 소개하면 linear function, activation function과 fourier transform을 이용해 neural operator을 구현한 것이다. 이 논문에서 주장하는 contribution은 다음과 같다.
- 나비에-스톡스 계열 방정식에 대한 resolution-invariant solution operator을 배운 첫번째 연구이다. 이전의 graph-based neural network는 수렴하지 않았다.
- 입출력 공간의 discretization과 상관없이 같은 네트워크 파라미터를 사용한다. lower-resolution에서 훈련한 결과가 higher resolution에서 evaluated 될 수 있다. (zero-shot super-resolution) 아래의 Figure 1을 참고하자.
- 이전의 deep learning method보다 성능이 좋다. 비교적 resolution이 작아 이전의 연구가 유리한 64x64 에서도 그렇다.
- 256x256 grid에서 나비에-스톡스에 대한 pseudo-spectral method의 2.2초보다 훨씬 빠른 0.005초에 inference가 가능하다. 이러한 속도상의 이점을 가지고도 정확도가 떨어지지 않아 Bayesian inverse problem 같은 downstream application에 이용할 수 있다.
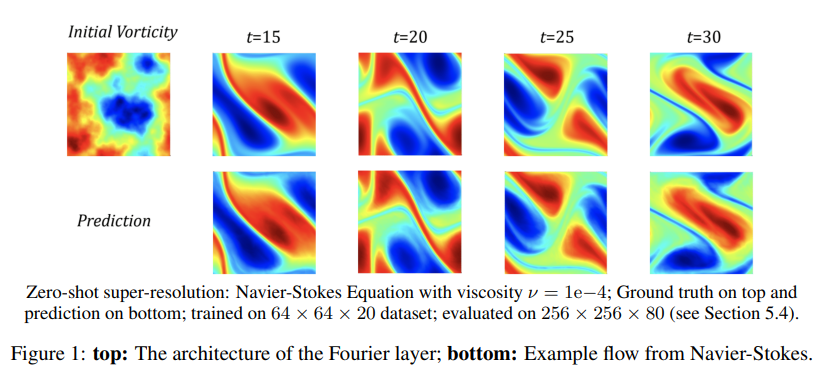
2. Learning Operators
일단 문제를 엄밀히 정의하자. 함수의 도메인은 bounded open set $D \subset \mathbb R^d$이고, Banach space의 $\mathcal{A}=\mathcal{A}(D; \mathbb{R}^{d_a})$와 $\mathcal{U}=\mathcal{U}(D; \mathbb{R}^{d_u})$ 사이의 map $G^\dagger: \mathcal{A} \rightarrow \mathcal{U}$를 neural network를 통해 근사하고자 한다. 이 때 우리는 observation ${a_j, u_j}$를 이용해 parametric map $G: \mathcal{A} \times \Theta \rightarrow \mathcal{U}$, 다시 말해 $G_\theta: \mathcal{A} \rightarrow \mathcal{U}$를 최적화한다. 더 자세한 내용은 논문에서 수학적으로 깔끔하게 정의해뒀으니 참고하자.

이 연구는 single instance $a \in \mathcal{A}$에 대한 $u \in \mathcal{U}$가 아닌, $G^\dagger: \mathcal{A} \rightarrow \mathcal{U}$을 neural network를 통해 근사하고자 한다는 점에서 기존의 연구인 PINN(Physics-informed Neural Network) 등과 다르다. 그래서 neural operator을 나름 굉장히 특색있는 연구라 생각한다. 참고로 PINN은 $(x,t) \mapsto u(x,t)$를 neural network로 근사하는 연구로 알고 있다.
3. Neural Operator
Neural operator[1:3]에서 neural operator을 다음과 같이 formulate한다.
입력 $a\in \mathcal{A}$에 대해,
- local transformation $P$를 이용해 $v_0(x)=P(a(x))$로 lift
- $v_0 \mapsto v_1 \mapsto \ldots \mapsto v_T$과 같이 iterative update
- local transformation $Q$를 이용해 $u(x)=Q(v_T(x))$로 projection
그리고 iterative update는 아래와 같이 formulate된다. 참고로 아래의 수식은 읽어보면 크게 복잡한 내용은 없지만 FNO을 이해하는데는 넘겨도 무리가 없으므로 그냥 넘어가도 된다.

$\mathcal{K}$는 non-local integral operator이고, $\sigma$는 local, nonlinear activation function이다.
그리고 $\mathcal{K}(a; \phi)$는 아래와 같이 정의되며,
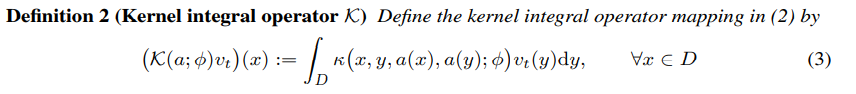
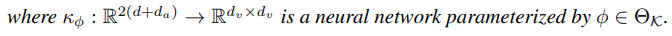
여기서 $\kappa_\phi$가 data에서 배울 kernel function이 된다.
위의 두 정의를 엮으면 Neural operator[1:4]에서 제시한 "무한차원 함수공간으로의 인공신경망의 일반화"를 이루게 되고, integral operator가 linear한데도 activation function과 같이 사용하며 복잡한 함수도 근사할 수 있다.
4. Fourier Neural Operator
위의 kernel integral operator에서 $a$에 대한 dependence를 지우고, $\kappa_\phi(x,y)=\kappa_\phi(x-y)$라 하면(kernel 함수의 특징상 크게 무리가 있는 가정은 아니다) $\mathcal{K}$는 단순한 convolution operator이 된다. Convolution operator을 효율적으로 계산하기 위해 원래 공간에서의 convolution은 fourier space에서의 hadamard product과 같음을 이용하며, 이게 FNO architecture의 핵심이다.
$$\begin{align}\left(\mathcal{K}(\phi) v_t\right)(x) &= \int_D \kappa_\phi(x-y) v_t(y)dy \\&=\mathcal{F}^{-1}\left(\mathcal{F}(\kappa_\phi) \cdot \mathcal{F}(v_t)\right)(x) \\&=\mathcal{F}^{-1}\left(R_\phi \cdot \mathcal{F}(v_t)\right)(x)\end{align}$$
물론 이것만으로 끝인 건 아니고, fourier transform 후 high-frequency modes들을 적당히 없애(truncate) $k_{max}$개만 남기는 작업도 수행한다. 이는 일종의 regularization으로 작용하는 것으로 보인다. 물론 논문 9p에서 high frequency는 복원될 수 있다고 주장하며, 자세한 내용은 있다 서술한다.
그 외에 discretization 방법, $R$의 parameterization($a$ 포함하도록) 등 디테일이 있으니 필요하면 읽어보자. Fourier Transform에는 FFT를 써봤고 매우 효율적이었다고 한다. (물론 standard FFT를 사용할 때는 uniform discretization이 필요하다.)
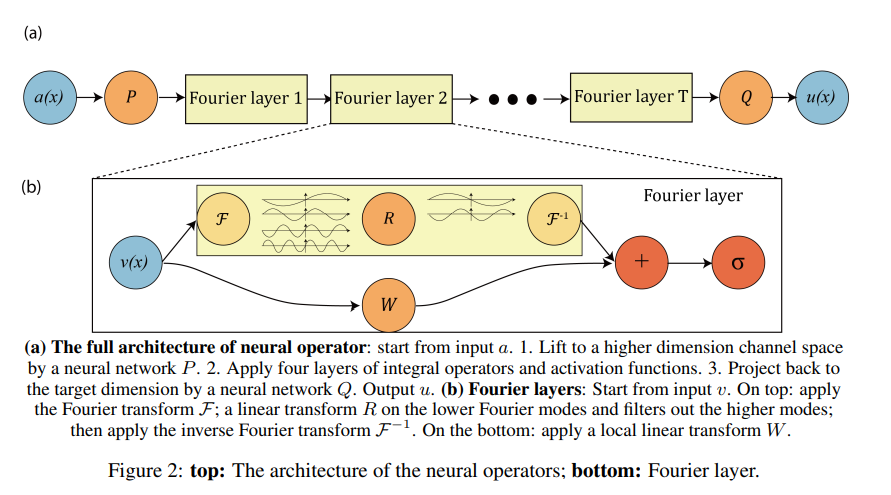
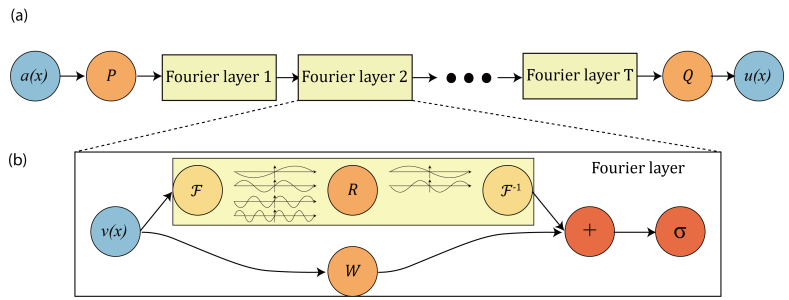
FNO의 전체 아키텍터는 위와 같다. 생각보다 매우 간단한 구조로 되어 있음을 확인할 수 있고, 소스코드를 찾아 읽어도 간단하다는 것을 확인할 수 있다. 참고로 Navier-Stokes, 2d 기준으로, $(x,y,t)$에 대한 함수를 다루는데, $P$에서는 $t$만 변하도록 1x1 convolution을 쓰고, Fourier layer에서는 $(x,y)$에 대한 fft-2d convolution-inv fft를 하고, $Q$에서는 $t$만 변하도록 1x1 convolution을 쓴다.
즉 세부 구현만 보면 "PDE"가 아니라 "Deep Neural Network"가 중심이다. 내부 구조를 보면 평소 보던 DNN과 그다지 다를 게 없다.
5. Numerical Experiments
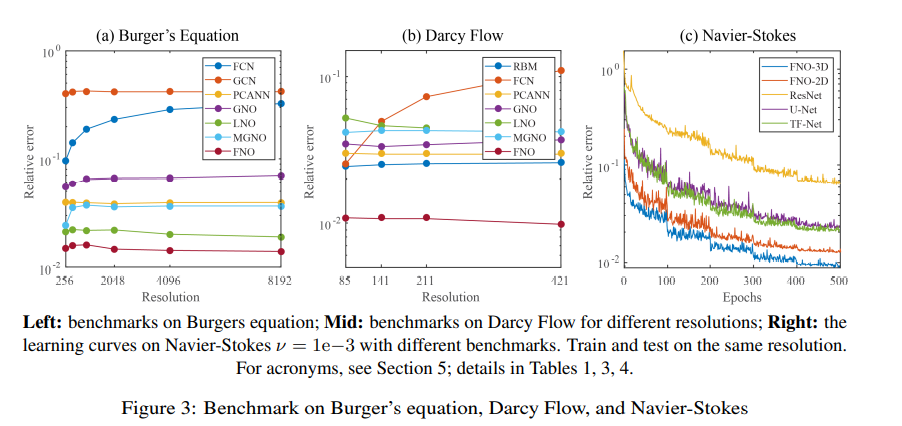
다른 방법보다 성능이 낫다는 그림이다. Burger's equation, Darcy flow, Navier-stokes를 다루고 detail 역시 설명하고 있으니 필요하면 읽어보자.
아래 Table은 Navier Stokes에 대한 benchmark이다. 특이하게도 FNO-3D 경우 $\nu=1e-5$와 $\nu=1e-4, N=1000$에서 데이터 부족으로 성능이 떨어지는 것을 볼 수 있다. 사실 이건 DNN 입장에서는 안 특이하고 (traditional) PDE solver 입장에서는 특이한 현상인데, PDE solver은 train data 수가 모자르든 말든 애초에 train의 개념 자체가 없어 generalization ability를 논의할 수조차 없다. DNN 입장에서 generalization ability는 항상 논의되는 개념이고 학습 데이터가 부족하면 성능도 떨어질 수밖에 없다.
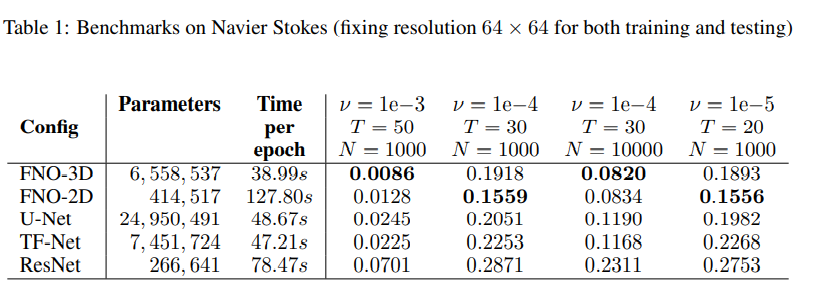
5.5 Bayesian inverse problem
$T=50$의 sprase, noisy observation이 주어졌을 때 initial vorticity를 추정했다. MCMC를 이용해 posterior distribution의 샘플을 그렸다고 한다.
결과, Figure 6를 보면 posterior mean은 거의 같고 late-time dynamic도 잘 복원하지만, FNO는 2.5분이 걸렸고 traditional solver은 18시간이 걸렸다고 한다. 물론 data generation, training time이 12시간이지만 이걸 고려해도 빠르다.
일단 훈련하면 inference가 빠르고, FNO는 미분가능하기에 PDE-constrained optimization problem에 adjoint method 없이 쉽게 적용될 수 있다고 한다. 이건 구체적인 예시도 있으면 좋을텐데, 후속 연구 중 이걸 다루는 게 있는지 모르겠다.
- integral operator 사이의 activation function이 high frequency mode를 복구하는 데 도움을 준다고 주장한다.
- linear transform $W$항이 non-periodic boundary를 다룰 수 있게 한다고 주장한다. Dary Flow와 time domain of Navier-Stokes를 예시로 든다.
6. Discussion and Conclusion
데이터가 중요하다, recurrent structure로 바꿀 수 있다(weight sharing을 통해), computer vision에 활용될 수 있다고 주장한다.
개인적인 의견을 덧붙이자면, 특히 PDE 경우 classical PDE solver로 훈련 데이터를 얻어야 하는데, 이건 classical PDE solver가 느려서 neural operator을 쓰겠다는 취지와 약간 충돌된다. 정작 classical PDE solver 대신 쓰겠다는 neural operator을 훈련하려면 classical PDE solver가 필요하기 때문이다.
또 training을 마친 후에는, 임의의 time에서 evaluation이 불가능하다는 것도 한계이다. training data와 test data가 비슷해야 결과가 잘 나온다는 것도 machine learning 특성 상 당연하고..
Recurrent structure에 대한 언급은 후속 연구인 FFNO(Factorized Fourier Neural Operator)에서 채택해 실험을 진행한 것으로 보인다.
그리고 computer vision은.. 이미 classical convolution layer 잘 쓰고 있는데 fourier transform을 적용할 일이 생길지? 뭐 어딘가 특별히 필요한 데가 있을지는 모르겠다. FNet 같은 연구를 전에 본 적은 있지만 그거 말고 본 건 없다.
A.2 Spectral Analysis
Navier-Stokes에 대한 spectral decay를 보여준다.
Implementation Details
논문 내용 외적으로, implementation을 살펴보며 보인 detail 몇가지를 소개하려고 한다.
1. fft shift
다차원에 대한 fft 결과는 lower frequency > high frequency 순서로 나오는 게 아니라, lower frequency가 앞과 뒤에 붙도록 나온다. (아래 그림을 참고하라) 거기다 last channel은 이게 적용이 안된다는 차이점까지 있다.
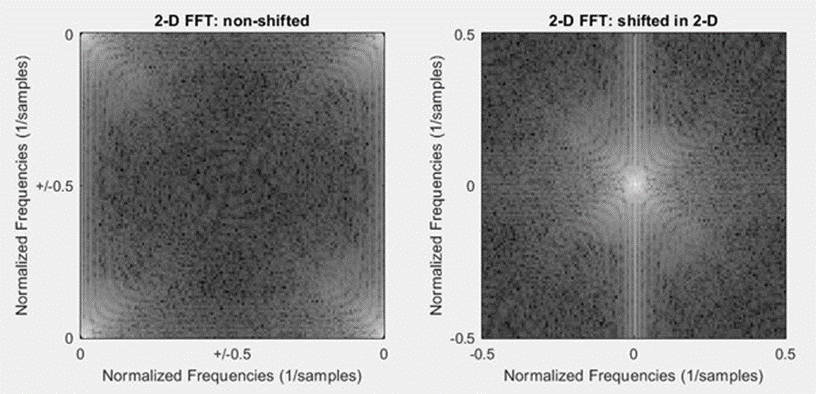
그래서 아래처럼 좀 이상하게(?) 인덱싱이 되어있다. 0부터 modes1까지, -modes1부터 0까지, ... 인덱싱해야 한다.
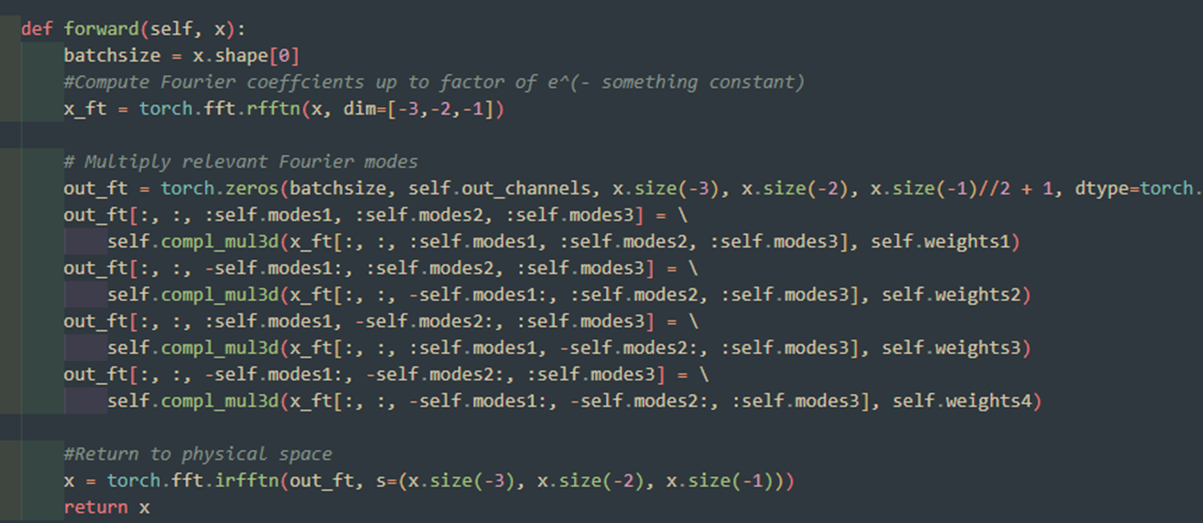
2. complex dim
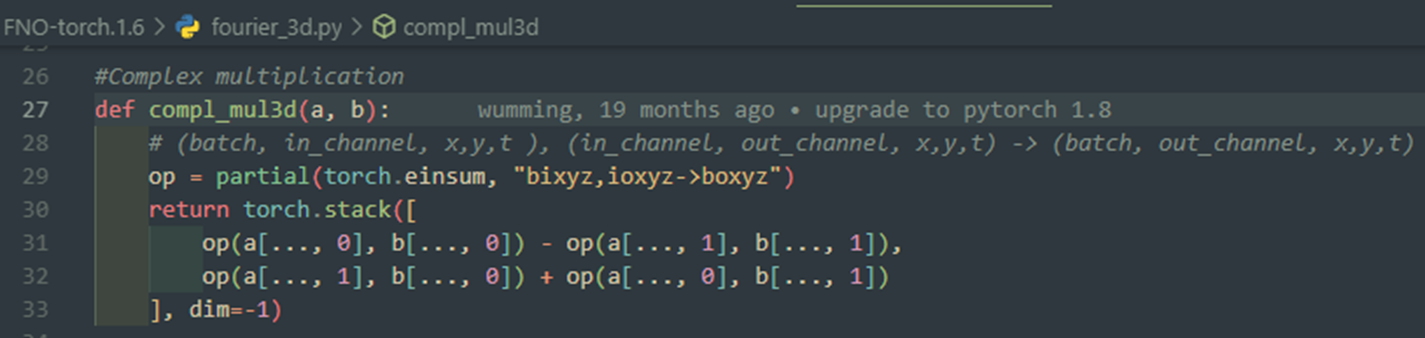
위는 토치 구버전 구현
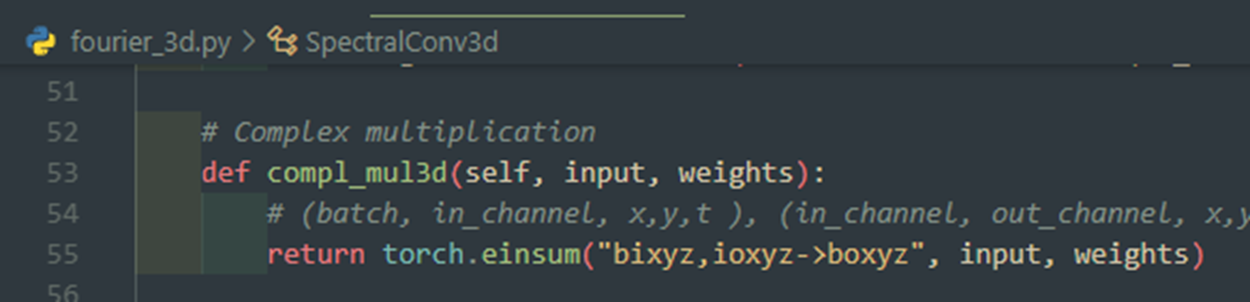
위는 토치 최신버전 구현
예전에 토치에서 복소수를 2차원으로 다뤄주던 것 때문에 생긴 이슈로 보인다.
Reference
내가 이 글을 쓰며 참고한 것들이다.
https://zongyi-li.github.io/blog/2020/fourier-pde/
https://youtu.be/IaS72aHrJKE
논문 [1:5], [2], 등등
이후 연구가 궁금한 사람은 FFNO(NIPS 2021)와 Transform Once: Efficient Operator Learning in Frequency Domain(ICML 2022)을 찾아보자.
Neural Operator: Learning Maps Between Function Spaces, https://arxiv.org/abs/2108.08481 ↩︎ ↩︎ ↩︎ ↩︎ ↩︎ ↩︎
Fourier Neural Operator for Parametric Partial Differential Equations, https://arxiv.org/abs/2010.08895 ↩︎