QAOA(Quantum Approximate Optimization Algorithm)
Quantum circuit 위에서 최적화 문제를 푸는 방법은 여러가지가 있지만 - 내가 최근에 흥미롭게 읽은 방법은 2가지이다. DQNN(Dissipative quantum neural networks)와 QAOA(Quantum Approximate Optimization Algorithm)이다. Quantum Neural Network에 대해 궁금하다면 Quantum Neural Network(Kerstin Beer, 2022)를 읽어보기를 권한다. 이 글에서는 QNN은 아니고 QAOA에 대해 간단히 소개할 예정이다.
양자컴퓨팅이나 양자역학에 대한 기본적인 지식을 필요로 한다.
QAOA
QAOA가 최적화 문제를 푸는 방법은 굉장히 간단하다.
- problem Hamiltonian $H_P$와 mixing Hamiltonian $H_B$를 찾는다. 이것들이 이미 알려진 문제들도 존재하고, 또는 정확히 모르더라도 후술할 범용적인 방식으로 construct할 수 있다.
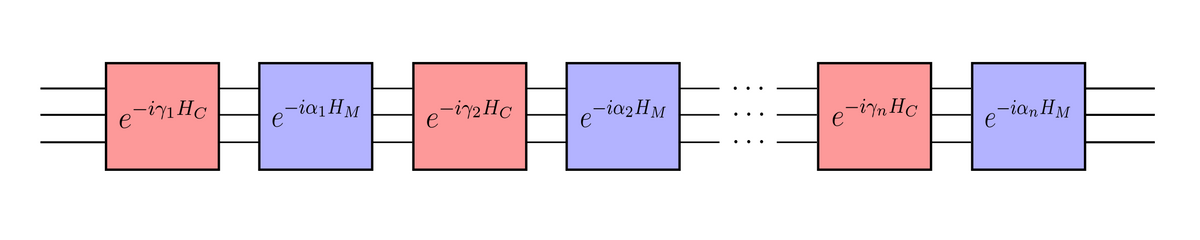
- 2개의 유니터리 게이트, $U(\beta)=\exp(-i\beta H_B), U(\gamma)=\exp(-i\gamma H_P)$를 정의한다.
- initial state $\ket{\psi_0}$에 대해, output state는 $\ket{\psi(\beta, \gamma)}=U(\beta_n)U(\gamma_n) \cdots U(\beta_1)U(\gamma_1) \ket{\psi_0}$가 된다. $U(\beta)U(\gamma)$는 여러번 반복하여 넣는다.
- output state가 원하는 출력이 되도록 loss를 구하고, 고전적인 최적화 방법(gradient descent 등등..)을 이용해 파라미터 $\beta_i, \gamma_i$를 최적화한다.
이렇게 하면 끝이다! 파라미터를 최적화하고, $\ket{\psi(\beta, \gamma)}$를 measure하면 해가 나온다.
More detailed explanation
그래서 위와 같이 problem Hamiltonian과 mixing Hamiltonian으로 게이트를 구축하고 최적화하는 것만으로 해가 나오는 이유는 뭘까?
problem Hamiltonian, 또는 cost Hamiltonian에서 나오는 time evolution은 최적화하고자 하는 문제의 cost(다시 말해 $\langle \psi | H_P | \psi \rangle$)를 보존한다. mixing Hamiltonian은 그렇지 않다. 이 두 해밀토니안에 의한 time evolution을 번갈아가며 적용하다보면 state에 대한 cost가 점점 감소해 최솟값에 다다르게 된다. 더 정확히는, 최적화가 잘 된다면, 최적화 과정에서 state에 의한 cost가 최솟값에 다다르도록 파라미터들이 최적화가 될 것이다.
아니면, problem Hamiltonian은 problem Hamiltonian basis에서 phase만을 바꾸고, mixing Hamiltonian은 phase와 amplitude를 바꾼다고도 설명할 수 있겠다. 참고
How to set Hamiltonians?
problem Hamiltonian은 우리가 원하는 조건을 만족할 때 $\langle \psi | H_P | \psi \rangle$, 즉 state $\psi$의 $H_P$에 대한 기댓값이 최소가 되도록 설정한다. 더 자세히는, 어떤 상태 $\ket{x}$에 대한 cost가 $C(x)$일 때, $H_P=\sum_x C(x) \ket{x} \bra{x}$로 둔다. cost에 기반해 자연스럽게 Hamiltonian을 구축했다고 할 수 있다. 실제로 회로상에서 구현이 쉬울지, $C(x)$를 어떻게 계산할지는 차치하고..[1]
mixing Hamiltonian은 단순히 모든 gate에 Pauli X operator을 적용하는 것을 통해 정의한다. 참고한 레퍼런스에서 다 이렇게 해서 보여줬는데, 다른 방법도 있겠지만, 적당히 괜찮은 걸 골라 관습처럼 사용하는 것으로 보인다.
Reference
https://pennylane.ai/qml/demos/tutorial_qaoa_intro.html
https://qiskit.org/textbook/ch-applications/qaoa.html
https://youtu.be/VTFJjDYXPOA
problem Hamiltonian이 $H_P=\sum_x C(x) \ket{x} \bra{x}$에서 더 간략화된 꼴로 나타내어지지 않는다면, 다시 말해 모든 state에 대한 cost $C(x)$를 따로 구해야 된다면, problem Hamiltonian을 구해서 QAOA를 하는 의미가 없을 것이다. 다행히도 Maxcut 등 여러 문제는 problem Hamiltonian을 $\sum_{(j, k) \in E} \frac{1}{2}(1-Z_jZ_k)$와 같이 조금 더 간략화시켜 나타낼 수 있다. ↩︎