다항함수 미적분 시간단축 공식
다항함수 미적분 시간단축 공식을 대충 문제풀이전략 수학2편으로 보면 된다.
수학II 다항함수 미적분 문제풀이 중에 습득한 몇가지 팁이 있다. 그에 대해 간략하게 정리한 글을 써보려고 한다.
한 점에서 근이 서너개 있다니 뭐니 하는 수학적으로 그다지 엄밀하지 않은 표현이 나오는데 느낌대로 이해해주면 된다. 그래도 설명을 덧붙이자면, x = α에서 근이 n개 있다는 말은 다항식이 \((x-\alpha)^n\)로 나누어 떨어진다는 뜻이다. 물론 이 때 n은 다항식이 나누어 떨어질 수 있는 최댓값일 것이다.
그리고 최고차항 계수를 a라고 할 때, a > 0인 경우만 다룬다. 넓이를 구해야 하는데, a < 0이면 알아서 − 1을 곱해주자.
1. 넓이
1.1 2차함수
2차 함수의 경우 근이 α, β로 2개 존재하면 (α < β), x축과 곡선이 이루는 넓이가 \(\dfrac{a(\beta-\alpha)^{3}}{6}\)인건 누구나 알 것이다. 증명이 궁금하면 그냥 f(x) = a(x − α)(x − β)로 두고 f(x)를 α부터 β까지 적분하면 된다.
1.2 3차함수1
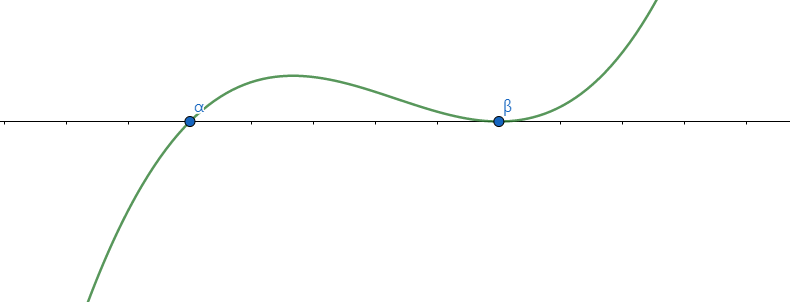
3차 함수는, 한 점에서 근이 2개 있고 나머지 하나가 다른 점에 존재하면, \(\dfrac{a(\beta-\alpha)^{4}}{12}\)이다.
1.3 4차함수1
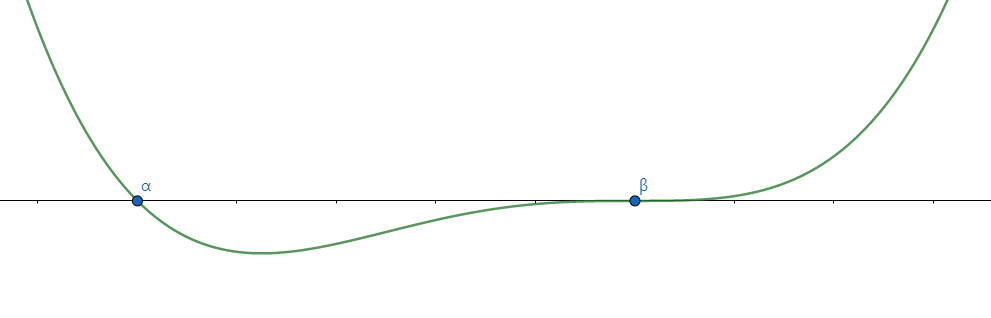
4차 함수는 한 점에서 근이 3개 있고 나머지 하나가 다른 점에 존재하면 \(\dfrac{a(\beta-\alpha)^{5}}{20}\)이다.
1.4 일반화
일반화도 가능하다. 논술 문제 중, 자연수 n과 실수 α, β에 대하여 \(\int_{\alpha}^{\beta}(x-\alpha)(x-\beta)^ndx\)를 구하는 문제가 있었다. 답은 \(\dfrac{(\alpha-\beta)^{n+2}}{(n+1)(n+2)}\)이다. 증명은 부분적분으로 쉽게 할 수 있다. 이건 넓이가 아니라 적분값이므로 음수가 나올 수도 있다.
아래는 두 근을 가지는 k차 다항식에 대한 일반화

1.5 3차함수2
이차함수는 축에 대칭이고, 삼차함수는 변곡점에 대해 대칭이다. 그런데 만약 삼차함수의 변곡점이 x축 위에 존재하면, 이 함수가 근을 3개 가진다면 변곡점은 x좌표가 변곡점과 다른 두 근의 중점에 위치한다. 말로 표현하려니 쓸데없이 어려운데 그냥 그래프를 그려보면 바로 무슨 말인지 알 수 있다.
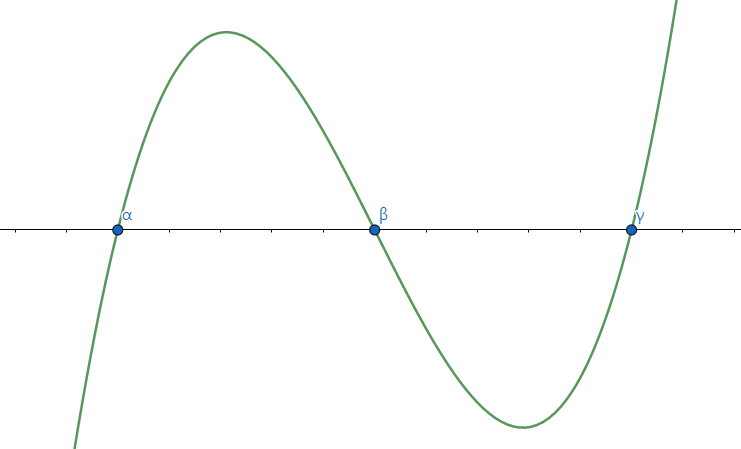
이러한 근을 α, β, γ라고 하면, 삼차함수가 x축과 이루는 도형을 생각하면 도형이 2개 나온다. 두 도형 중 하나의 넓이는 \(\dfrac{a(\beta-\alpha)^{4}}{4}\)이다. 쉽게 생각하면 거리를 네제곱하고, 4로 나누고 계수를 곱하면 된다.
두 도형의 넓이의 합, 다른 말로 삼차함수가 x축과 이루는 넓이는 \(\dfrac{a(\beta-\alpha)^{4}}{2}\)이다.
삼차함수와 x축이 이루는 넓이를 구할 때 일부 경우 유용하게 써먹을 수 있다.
1.6 4차함수2
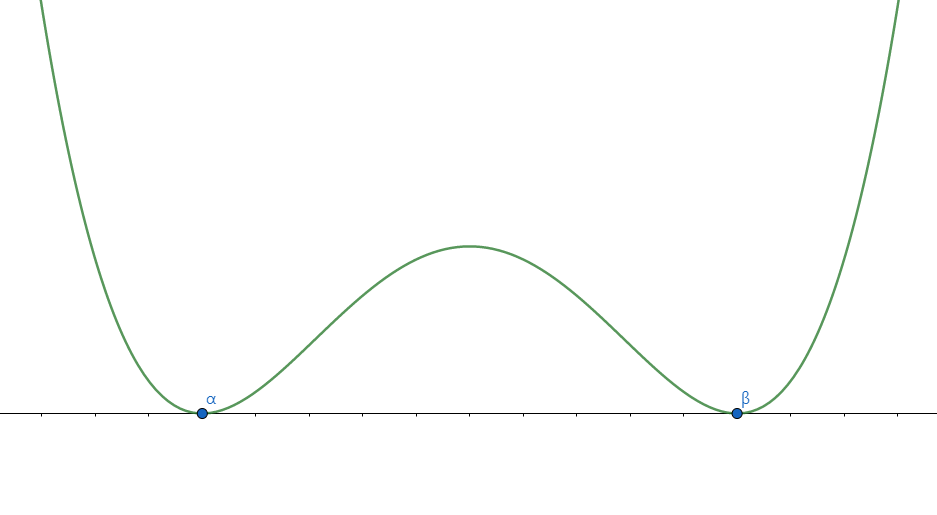
4차함수, 편의상 최고차항 계수가 양수인 4차함수를 생각하자. 이 4차함수의 극솟값이 0으로 같고, \(x=\alpha,\beta\)에서 극솟값을 가지면(α<β) 4차 함수과 x축이 이루는 넓이는 \(\dfrac{a(\beta-\alpha)^{5}}{30}\)이다.
쓰이는 경우는 흔하지 않지만, 내가 한 3번 정도 이걸 쓰는 문제를 봤는데 사차함수 적분의 특성상 일일이 적분하고 앉아있는 것보다 시간을 월등히 절약할 수 있다.
2. 극점
2.1
3차함수가 한 점에서 x축을 뚫고 나오고 (x = α), 한 점에서 x축과 접하면 (x = β) 극점의 x좌표는 (α, 0)과 (β, 0)의 1:2 내분점의 x좌표와 같다.
4차함수에서 근이 하나는 x = α, 3개는 x = β에 있을 때도 비슷하게 1:3 내분점에 극점이 있다.
간단하게 일반화할수도 있다. 다만 5차 함수 이상은 보통 볼 일이 없다.
2.2
삼차함수의 변곡점이 x축 위에 있고 근이 3개일 때, (변곡점에서 극점까지의 거리) : (변곡점에서 다른 근 까지의 거리) = \(1 : \sqrt3\) 이다.
생각보다 많이 유용한 팁이다. 활용하는 문제가 은근히 적지 않다.
3. 활용
위 공식을 그대로 경우에 맞게 적용해서 쓸 수도 있고, 삼차함수와 관련된 특징이 좀 많은데 삼차함수를 미분했을 때 이차함수가 나오는 점을 활용할 수도 있다. 간단한 예를 몇가지 적어줬는데, 3.1와 3.2는 내신형 노가다 문제 중에 자주 나온다. 예시로 적어둔 활용 방법 외에, n차 함수를 미분하면 n-1차 함수, 적분하면 n+1차 함수가 나오고, 어떤 원시 함수의 두 함숫값의 차가 피적분함수의 적분값과 같다는 점을 이용해 다양한 곳에 활용해 시간 단축을 할 수 있다. 쉽게 말하면 어떤 함수에서 높이 차이(함숫값 차이)는 피적분함수의 넓이(정확히는 적분값의 절댓값)인 것을 이용하면 된다.
3.1
이차함수의 f(x) = 0의 두 근이 x = 0, 1에 있을 때, \(\int_0^{a}f(x)dx=0\)인 a의 값을 구하는 문제를 생각해보자.
원래대로라면 f(x) = kx(x − 1)라고 두고 f(x)를 정적분해서 해를 찾는 쓸데없이 귀찮은 문제다.
위의 팁 중 2.1을 이용하자. f(x)의 원시함수를 F(x)로 하고, F(x) = 0라고 해서 그래프를 그려보면 0부터 a까지 f(x)의 적분값이 0이므로 삼차함수의 두 근은 x = 0, a이다. 이 때, 2.1에 의해 (0, 0)과 (a, 0)의 2:1 내분점이 극점 (1, 0)이므로 a = 1.5이다.
3.2
이차함수의 두 근이 x = − 1, 1일 때, \(\int_0^{a}f(x)dx=0\)인 a를 구하는 문제를 생각해보자.
원래대로라면 f(x) = k(x − 1)(x + 1)라고 두고 정적분해서 해를 찾아야 한다.
위의 팁 중 2.2를 이용하자. 예제 3.1과 마찬가지로 F(x) = 0으로 해서 이차함수를 적분한 그래프를 그려보면, x = − 1, 1에서 극점을 갖고 원점에 대해 대칭인 삼차함수가 나온다. 이 때, 2.2에 의해 \(a=\sqrt3, -\sqrt3\)이다.
3.3

이차함수 넓이 공식을 이용해서 풀 수 있는 문제이다. 답은 4이다.
3.4

이차함수 넓이 공식을 이용해서 풀 수 있는 문제이다. 답은 2번이다.
3.5
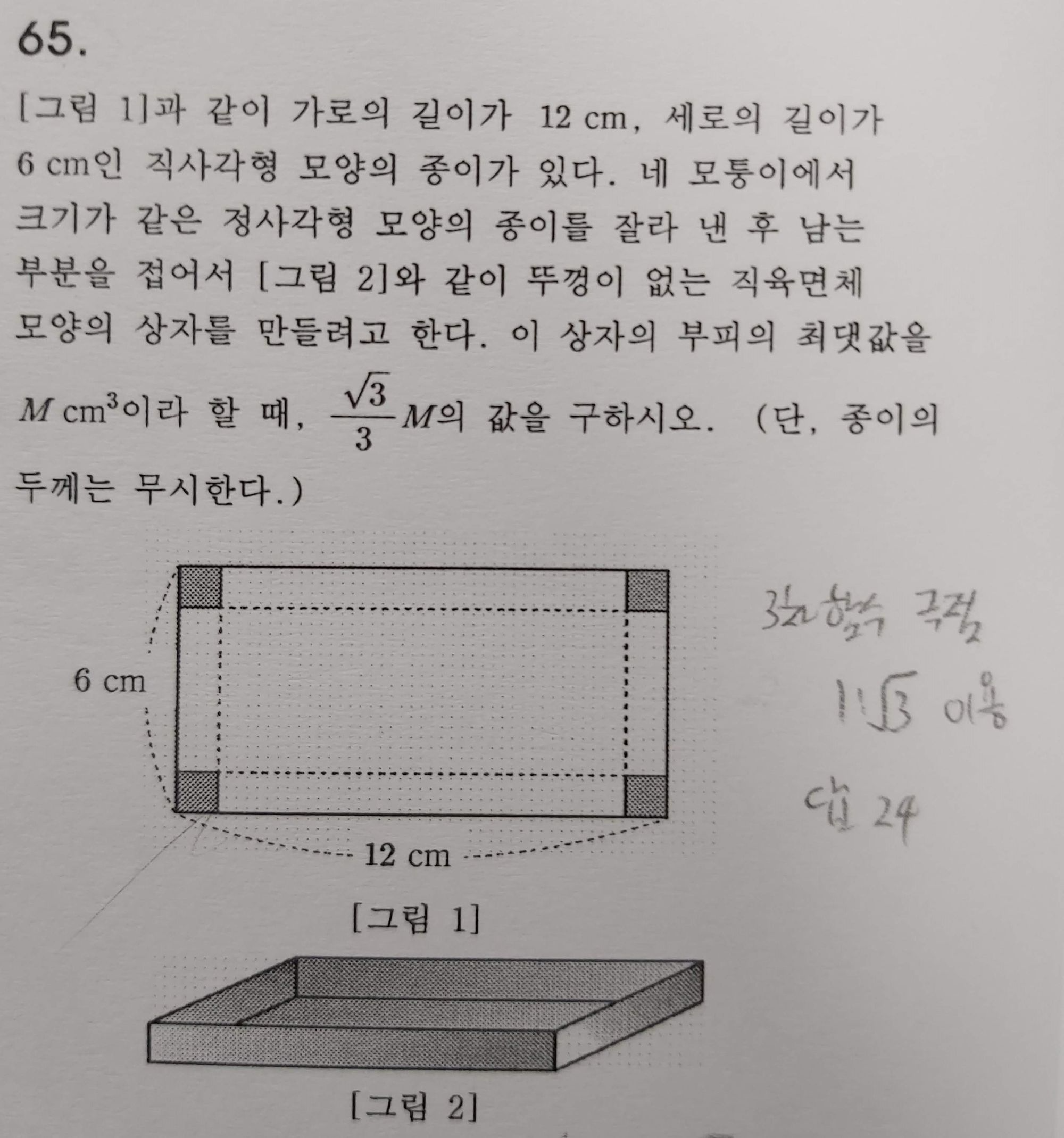
이런 유형의 문제는 변수 잘 잡은 다음 문제에서 구하라고 하는 넓이/부피 등을 변수로 잘 나타내고 변수 범위 주의하면서 풀면 된다. 요령이 있으면 굉장히 빨리 풀 수 있는 유형의 문제이다. 삼차함수를 처리하기 쉽게 변곡점이 원점이 되도록 평행이동 시킨 후에 변곡점에서 극점까지의 거리와 근까지의 거리 비 \(1:\sqrt3\)을 활용하면 쉽게 풀 수 있다. 답은 24이다.
3.6
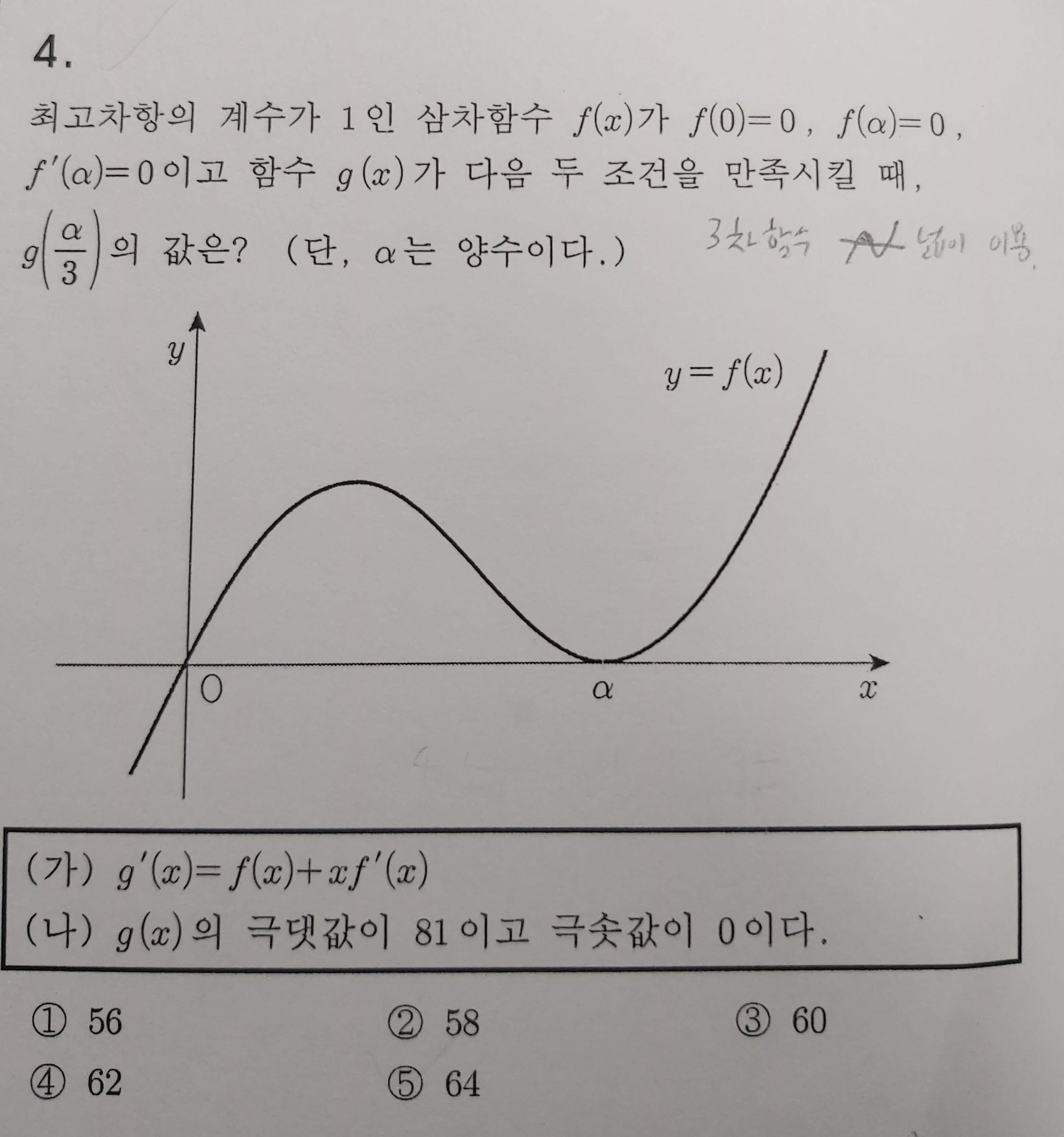
본문의 1.5 3차함수의 넓이 - 근에서 변곡점까지 버전으로 풀면 나름 빠르게 풀린다. 답은 5번이다.
3.7
솔직히 그닥 좋은 예는 아니지만, 2017 수능 30번을 풀 때 끝 부분 자잘한 계산을 생략할 수 있다. 2017 수능 30번을 풀다보면, 삼차함수가 원점 대칭이고 근이 \(0, 3\sqrt3, -3\sqrt3\)에 있고 최고차항 계수가 -4일 때 극댓값의 값을 구해야 답이 나온다.
쓸데없이 자잘한 귀찮은 계산해서 풀지 말고, 삼차 함수 \(h(x)=-4x(x^2 -27)\)라고 했을 때 극대/극소가 x = 3, − 3에 존재하므로 (본문의 2.2) h(3)을 구해야 하는데, h(3) = 216이 답이 된다.
근데 예시랍시고 써놓고 보니 그냥 미분해서 풀어도 시간상 그닥 큰 차이가 없는 예시다.
마무리
수학 준킬러, 킬러 문제중에 풀이 과정 중 다항함수 미적분을 사용하는 문제가 적지는 않은데 하나 하나 다 노가다로 계산하는 데 걸리는 시간을 이러한 잡다한 공식으로 줄일 수 있다. 그러나 중요한 건 이러한 공식, 즉 도구가 아니라 도구를 사용하는 사람이다. 이러한 공식을 아무리 많이 잡다하게 알고 있다고 한들 문제에 제대로 정확히 활용하지 못하면 그다지 쓸모가 없다. 꾸준한 문제풀이를 통해 공식 응용에 숙달할 수 있도록 하자.
아, 그리고 음의 적분값 구할때 넓이 공식 사용해놓고 틀리지 말자. 넓이는 0 이상이다. 최고차항 계수 곱하는 것도 주의하고, 최고차항 계수가 음수일 때는 넓이가 음수가 되는 경우를 주의하자.