문제풀이전략 수학1
다항함수 미적분 시간단축 공식을 대충 문제풀이전략 수학2편으로 보면 된다.
1. 개요
수학1 문제를 풀어낼 때 유용한 팁 몇가지를 소개하는 글입니다. 2번과 3번은 실전적인 문제풀이에 상당히 도움이 되지만 4번과 5번, 이진트리와 이진법은 지적유희에 더 가깝습니다. 알면 좋고 몰라도 문제 못 푸는 거 아닙니다.
2. 0.5번째 항
등차수열에만 쓸 수 있습니다. 등차수열이 아닌 수열(대표적으로 등비수열)에 쓰고 왜 답이 안 나올까 고민하시면 안됩니다.
$$\sum^n_{k=1}a_k=S_n=na_{n+1 \over 2}$$
말로 바꿔서 이해하면 첫 번째 항부터 n번째 항까지의 합은, 그 중간번째 항의 n배입니다.
굳이 초항부터 합할 필요도 없습니다. 예를 들어 7번째 항부터 15번째 항까지의 합은, 7과 15의 평균은 11이기에, \(9a_{11}\)입니다.
$$\sum^a_{k=b}a_k=S_a-S_{b-1}=(a-b+1)a_{a+b \over 2}$$
1번째 항부터 10번째 항까지의 합은 \(10a_{5.5}\)입니다. 시중 실모를 있는대로 풀다보면 10번째 항까지 합한 걸 물어보는 경우가 많아서 가장 많이 보는 형식일 겁니다.
이게 왜 쓸모가 있냐고요? 소위 “정석적인 풀이”를 쓰다가 이 팁을 잘 쓸 수 있게 되면 차이가 확 체감되실겁니다. 등차수열인 이상 항상 성립하기 때문에 단순한 2점 문제에서부터 4점 문제까지 어디든지 적용할 수 있습니다.
자매품으로 0번째 항과 음수번째항이 있습니다. 마찬가지로 자연수 n에 대해서만 정의되는 수열을 해석적으로 확장한 개념입니다. 그러나 음수번째 항은 손으로 표기할 때 약간 번거로워서 보통 안 씁니다.
3. 함수로의 해석과 그래프, 미분/적분
이 팁 역시 등차수열에만 적용 가능합니다.
등차수열의 합 수열은 항상 다음과 같은 꼴입니다.
$$S_n=an^2+bn$$
등차수열의 교과서 정의에 따르면 \(a=0\)이어도 안 될 것은 없습니다만 문제로서 의미가 있으려면 거의 모든 문제에서 \(a\ne0\)이라고 제시할겁니다. 아무튼 합 수열의 중요한 성질은 다음과 같습니다.
상수항이 무조건 0입니다. 상수항이 0이 아닐 경우, \(a_n\)은 ‘초항만 등차수열이 아닌 수열’로 보통 문제에 나올 겁니다. 이때는 반드시 초항을 따로 처리해줘야합니다. 내신 때 자주 보는 예시이죠.
\(S_n\)을 n에 대한 함수로 해석하고 n을 실수로 확장하고 x축이 n을 나타내는 그래프를 그렸을 때, 이 그래프는 항상 원점을 지납니다. 즉, \(S(0)=0\)입니다.
그래프로 그렸을 때 대칭축은 \(a_n=0\)인 n에 있지 않습니다. 합 수열을 미분한 식과 \(a_n\)이 다르기에 나타나는 차이입니다. \(a_n=0\)인 \(n\)이 존재할 때, \(S_n\)의 대칭축은 \(n-0.5\)에 위치합니다.
이거 헷갈려서 실수하지 마세요.
그런데, 미분과 적분을 배울 적에 미분은 변화량이고 적분은 쌓아서 더하는 것이라 배웠습니다. 그럼 당연히 \(a_n\)과 \(S_n\)사이에도 관계가 있지 않을까요? 저는 이런 의문을 가지고 \(S_n\)을 다음과 같이 나타내보았습니다.
$$S_n=\int^{n+1}_1 a([x])dx$$
\(a(x)\)는 \(a_n\)에서 n을 실수 범위로 확장하여 해석한 함수, 즉 일차함수입니다. 보시면 알겠지만 놀랍게도 위 식은 문제풀이에 전혀 써먹을 수가 없습니다. 그런데 도대체 왜 갑자기 알려줬냐고요? 그냥 저렇게 표현할 수도 있다.. 정도를 알려주고 싶었습니다. 네 근데 문제 풀 때는 쓸모 없어요.
아무튼 합 수열에서 원래 수열을 유도하거나, 그 역 과정을 수행하는 과정은 아래와 같습니다. 공식이 존재하기 때문에 그냥 공식 암기해도 상관 없는데 암기하기는 싫어서 적당히 자기 자신과 타협한 방법입니다. 미분/적분과의 연관성을 만들고 싶은 마음도 있었습니다.
보시면 아시겠지만 사실 미분/적분을 통해 최고차항 계수를 양방향으로 구할 수 있다는 것 말고는 유효한 게 없습니다.
\(S_n=an^2+bn\)일 때 \(a_n\)을 구하고 싶다면,
- \(S_n\)을 \(n\)에 대해 미분한다.
- \(a_1=S_1\)을 이용해 \(a_n\)의 상수항을 구합니다.
\(a_n=an+b\)일 때 \(S_n\)을 구하고 싶다면,
- \(a_n\)을 \(n\)에 대해 정적분하되, 상수항을 0으로 맞춘다.
- \(a_1=S_1\) 이용
활용성은 무한하고 잘 쓰면 굉장히 큰 시간적 이득을 볼 수 있습니다만, 활용을 구체적으로 어떻게 할 지는 독자에게 맡기겠습니다.
4. 이진트리 (수형도)
이진트리는 이산수학/프로그래밍 할 때 자주 쓰는 용어이고, 더 보편적인 개념으로 중/고등학교 때 배우는 개념은 수형도입니다.
이진트리에서는, 보통 n번째 항 아래의 두 ‘자식’으로 2n번째 항과 2n+1번째 항을 가집니다. 아래 그림을 보면 어떻게 생긴 것인지 알 수 있습니다. 물론 복잡하게 ‘이진트리’라는 개념을 알 필요도 없습니다. 그냥 ‘수형도’로 이해하셔도 전혀 문제풀이에 지장 없습니다.
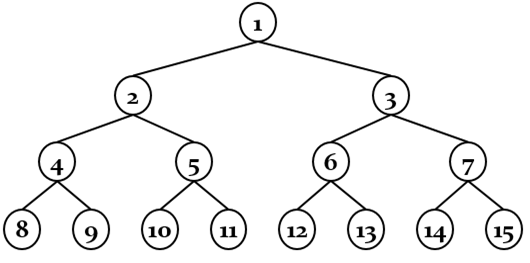
\(a_{2n},a_{2n+1}\)을 \(a_n\)으로 이루어진 식으로 나타낸 문제의 경우 이진트리를 사용하면 유용한 경우가 종종 있습니다. 그 이유는 이게 첫 번째 항부터 2의 거듭제곱수번째의 항까지 나타내기에 편리한 방법이기 때문입니다.
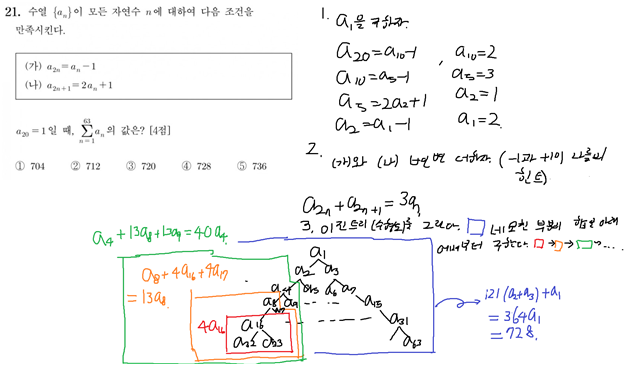
201121(나형)입니다.

비슷한 문제인 21사관(가형) 18번입니다. 똑같이 이진트리를 그려서 풀 수 있습니다. (가)와 (나)를 변변 더하면 양변에 2n+1, 2n+2번째 항과 n+1번째 항이 남습니다. 이진 트리의 가장 위 노드를 \(a_2\), 아래 자식 2개를 \(a_3,a_4\)로 두어도 문제 풀이에 큰 지장은 없습니다만, 먼저 풀었던 문제처럼 풀고 싶으시면 2n+1을 (2n)+1로, 2n+2를 (2n+1)+1로, n+1을 (n)+1로 해석하면 됩니다. 그럼 이제 원래 알던, 루트(최상위 노드)가 1인 이진트리와 다를 게 없다는 걸 알 수 있죠? 201121(나형)과 거의 유사하게 풀어낼 수 있습니다. 오히려 초항을 유도해내는 과정이 없기에 더 쉽겠죠.
5. n진법
먼저 이것부터 말하겠습니다. 이진법은 교육과정에서 빠진 지 몇 년 지났습니다. 즉, 몰라도 문제풀이에는 지장 없습니다. 다른 방법으로 충분히 풀 수 있습니다. 다만 다양하고/더 간단한 풀이를 위해 보여드리는 것 뿐입니다.
그러나 평가원에서도 계속 n진법을 잘 알고 활용할 수 있으면 풀이가 쉬운 문제를 출제하고 있고, 사설에도 자주 나오는 소재이므로 n진법과 그의 문제풀이에의 활용법을 미리 알고 있으면 도움이 될 겁니다. 1등급을 넘어 100점이 목표라면 충분히 알아둘 만 해요.
위 글에 n진법이 뭔지에 대한 간략한 설명에다 211121의 간략한 풀이도 덧붙였으니, 참고 바랍니다.
프로그래밍을 해보신 분이라면 거의 당연히 이진법에 대해서는 알 텐데 이 관점으로 문제를 바라보는 과정을 보면 매력을 느끼실 수 있을 겁니다. 이진법에 대해서는 이 칼럼에서 소개할 생각은 없고, 말 그대로 우리가 평소에 쓰는 10진법과 쓰는 숫자의 개수만이 다를 뿐이니 찾아보시면 금방 배우실 수 있습니다.

2021학년도 수능특강 수학1 수록문제입니다. \(a_{2n},a_{2n+1}\)과 \(a_n\)이 등장하는데, 이런 형태의 항을 주는 수열 문제는 대부분 이진법으로 해석할 수 있습니다. 만약 n이 이진법으로 나타냈을 때 문자열 ‘S’라면, 2n은 ‘S0’이고, 2n+1은 ‘S1’이기 때문입니다. (이진수에서 0을 붙이는 건 2를 곱하는 연산과 같습니다) ('S0', 'S1' 등의 표기는 단순 string concatenation입니다)
그러면 주어진 문제의 조건에 따라, \(a_6\)을 구해봅시다. 6은 이진수로 나타냈을 때 110이고, 문제의 조건에 의해 이진수로 나타낸 문자열 뒤쪽에 ‘1’을 붙일 때만 1을 더합니다. 즉 \(a_{11(2)}=2\)이고, \(a_{110(2)}=a_{11(2)}=2\)입니다. 말로 해석하면, \(a_n=\)(n을 이진수로 나타냈을 때 1의 개수) 로 해석할 수 있습니다.
이제 답을 도출해봅시다. 십진수 100은 이진수로 1100100입니다. 0부터 1100100(2)까지 1이 2개만 들어간 수를 세면 답이 나옵니다. 110010은 7자리니까, 7자리 중 1이 들어갈 2자리를 택합니다. 경우의 수는 \(7C2=21\)가지입니다. 이중 110010보다 숫자가 커지는 경우를 제외해야 하는데, 110010은 7자리 중 2개 자리에만 1을 넣은 그 어떤 수보다 큽니다. (7자리 중 2개 자리에만 1을 넣은 수 중 가장 큰 수는 110000(2)=96이기 때문입니다) 즉, 십진수로 100보다 수가 커지는 경우를 제외할 필요가 없습니다. 따라서 답은 그대로 21가지입니다.