문제풀이전략 미적분
다항함수 미적분 시간단축 공식을 대충 문제풀이전략 수학2편으로 보면 된다.
1. 개요
수능 대비에 있어 중요한 건 중요도 순서대로 N축-정적분 스킬이고, 나머지는 사실 몰라도 상관 없습니다.
수학적 유희 정도로 봐주세요.
2. 정적분 스킬
$$g(t)=\int^{12}_0|f(x)-t|dx$$
위 함수의 최댓값을 구해야 하는 문제를 쉽게 푸는 방법입니다. (이 때 \(f(x)\)는 연속이고, 미분가능이고, 하여튼 고교과정에서 다루기 쉬운 좋은 함수라고 가정합니다.)
$$f(x)-t_0>0$$
결론부터 말하겠습니다. \(f(x)-t_0>0\)을 만족하는 구간의 길이(이 때 구간의 길이는 \(x\)에 대해 구해야 하겠죠.)와 \(f(x)-t_0<0\)인 구간의 길이가 같은 어떤 \(t_0\)가 존재한다면, \(g(t)\)는 \(t=t_0\)에서 극값을 가집니다.
또한 평가원/교육청 문제라면 이러한 \(t=t_0\)에서 \(g(t)\)가 최댓값을 가질 확률이 높습니다.
그 이유를 알아봅시다.
https://cafe.naver.com/pnmath/1950139
이 글에서 잘 설명하고 있습니다만, 증명과정을 간소화해보겠습니다. 엄밀성은 내다 버린 증명이니 그냥 아 그렇구나 정도로 알아두세요. \(g(t)=\int^{12}_0|f(x)-t|dx\)의 극값을 구할 때, \(\frac{d}{dt}g(t)=0\)일 것입니다. 그럼 t가 아주 약간 변할 때 \(g(t)\)의 변화량이 0에 수렴할 것입니다. 편의상 t가 아주 약간 증가한다고 할 때, \(y=f(x)\)와 \(y=t\)를 비교해봅시다. \(x\)에 대해 \(f(x)-t>0\)인 구간에서는 이 구간의 길이가 \(l\)이면 \(g(t)\)가 \(ldt\)만큼 줄어듭니다. \(x\)에 대해 \(f(x)-t<0\)인 구간에서는 이 구간의 길이가 \(l\)이면 \(g(t)\)가 \(ldt\)만큼 증가합니다. 따라서 \(f(x)-t_0>0\)인 구간의 길이와 \(f(x)-t_0<0\)인 구간의 길이가 같은 어떤 \(t_0\)가 존재하면, \(t=t_0\)일 때, \(\frac{d}{dt}g(t)=0\)입니다.
3. N축
2020년에 제가 이걸 배울 때 커뮤니티에서 누군가가 수학 100점이 목표가 아니면 배울 필요가 없는 테크닉이라고 말한 적이 있습니다. 또 누군가는 합성함수를 그렇게 우려먹었는데 설마 또 나오겠어? N축도 필요 없겠지~라고 말한 적이 있습니다. 그런데 그 해에 나온 2021학년도 수능 수학 가형 30번만 봐도 아시겠지만 합성함수입니다. 합성함수 또 나왔습니다. N축으로 쉽게 풀립니다.
그냥 100점 목표 그런 거 필요 없고 1등급 목표면 알아두는 게 좋다고 봅니다. 알아둬서 나쁠 게 뭐가 있나요.
배우는 건 어렵지 않습니다. 유튜브든 현장강의든 뭐 누구한테서든 일단 배워와서 문제에 응용해서 적용하는 법만 체화하면 됩니다. 참고로 한 번 합성한 함수뿐만 아니라 두 번, 세 번 합성한 함수도 두 번 합성한 함수 그리는 요령과 똑같이 그려나가면 똑같이 N축 적용할 수 있습니다. f(g(h(x)))라고 하면 f(x)그래프 그려서 거기 아래에 g(x) 연결하고, g(x) 에 또 연속적으로 h(x) 연결해 그리면 됩니다.

그리고 보통 겉함수에서 극값(겉함수에서 x입장)을 아래 그래프로 점선으로 쭉 내려서 속함수에서 y값이랑 대응시키든지 하는 방식으로, 겉함수-속함수 사이에 극값 같이 특징적인 값들을 점선으로 이어주면 보기 편합니다.
4. 라이프니츠 미분법
사설 문제 풀다가 가끔 쓸모 있었습니다. 정적분 구간의 위끝 아래 끝에 변수가 들어가거나/정적분 대상인 피적분함수가 이변수함수일 때 가끔 쓸모 있습니다.
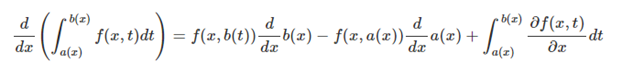
증명은 여기 참고
사설에서는 보통 정적분 구간의 위끝 아래끝 둘 중 하나가 상수이거나 둘 다 상수로 나옵니다.
활용법은 잘 고민해 보세요 소프트한 활용법 예시는
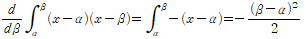
이 식을 이용해 이차함수 넓이 공식을 유도하는 https://cafe.naver.com/pnmath/2245250
5. 스케일 변형
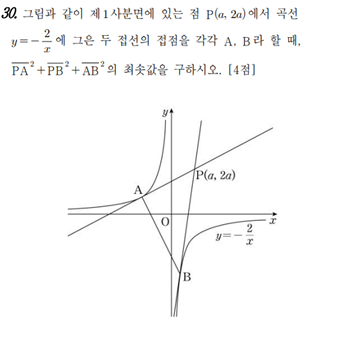
저 문제에서 공간을 y축 방향으로 길이가 1/2, 즉 절반이 되게끔 찌그러뜨려봅시다. 그럼 이 문제의 본질에 변화가 있을까요?
위의 문제에서, y축 방향의 길이를 절반이 되게끔 찌그러트리면, P(a,a), y=-1/x가 될 것입니다. 그리고 구하라는 최솟값을 구하려고 할 때 직관적으로 A, B는 원점에 대칭적인 위치에 있겠죠. 이러한 사고를 따르면 문제를 풀기가 꽤 쉬워집니다.
그리고 구하라는 최솟값을 구한 후에, 다시 y축 방향의 길이가 2배가 되게끔 늘려줘야 합니다. 그런데 구한 최솟값은 길이 제곱의 합이죠? (0,0)에서 (1,1)까지 거리의 제곱은 2이고, (0,0)에서 (1,2)까지 거리의 제곱은 5입니다. y축 방향 길이가 2배가 될 때 길이 제곱이 \(\frac{5}{2}=2.5\)배가 된 걸 눈치채셨죠? (물론 찌그러진 좌표계에서 구하는 길이가 모두 대각선 방향이나 역대각 방향인 게 한몫합니다)
실제로 y축 방향으로 길이를 절반으로 찌그러뜨리고 구한 답에 2.5를 곱하면 원래 문제의 답이 나옵니다.
이 문제를 이렇게 풀어도 되는 핵심적인 이유는, 좌표축 스케일을 이렇게 1/2로 변형한다 한들 두 함수가 "접한다"는 사실이 변하지 않기 때문입니다. 이렇게 불변량에 집중해 문제를 푸는 것은 물리와 수학에서 매우 중요하고, 흔한 사고입니다.
예제 문제 하나만 더 알려드리겠습니다. 이창무T 클맥 N제에도 있던 문제입니다.
\(\frac{x^2}{4}+\frac{y^2}3=1\)인 타원에 대해 \(x=1, x=-1\)과 타원으로 둘러싸인 도형의 넓이를 구해라.
x축 방향으로 타원을 1/2, y축 방향으로 타원을 \(1/\sqrt3\) 길이가 되도록 찌그러트려봅시다. 그럼 타원이 원이 되었습니다! 원은 당연히 넓이를 구하기 매우 쉽습니다. 정적분을 할 필요도 없이 그냥 기하적으로 생각하면 됩니다. \(x={1\over2}, x=-{1\over2}\)과 원으로 둘러쌓인 부분의 넓이를 구하고 \(2\sqrt3\)을 곱하면 \(\frac{2\sqrt3}{3}\pi+3\)이 답으로 나올 것입니다.
정해(?)대로 풀고 싶으면 y를 x에 대한 식으로 정리하고, 정적분하면 됩니다. 물론 음함수를 양함수로 바꾸는 과정에서 y가 음수인 부분이 상실되었다면 2배를 곱해줘야 합니다.
대학교 가서 미적분학을 배우면 카발리에리의 원리, jacobian matrix 등을 배우는데 이런 것들 배우고 이 문제의 풀이법을 다시 보시면 왜 이렇게 풀어도 되는지 조금 더 감이 잡힐지도 모르겠습니다. 더 나아가 물리학과면 metric 배우고 민코프스키 공간 같은 걸 배울거에요.
6. 손가락 가리기
내신에서는 가끔 쓸모 있는 팁입니다. 수능 대비하면서는 한번도 안 써봤습니다.