By MilkClouds in Differential Equations — 2022년 1월 25일

미분방정식 정리 01 - 미분방정식의 정의, 분류, 수치적 해법, Seperable First-order Equation, Linear First-order Equation

정의

\[L\frac{d^2q}{dt^2}+R\frac{dq}{dt}+\frac{q}{C}=\epsilon_0 \cos{\omega t}\]

위 방정식과 같이, 독립변수에 대한 미지의 함수(종속변수)와 그 도함수로 이루어진 방정식을 '미분방정식'이라 한다.

수치적 해법

Euler Method

$\frac{dy}{dx}=f(x,y)$임을 알고 있을 때, 아래 수식을 iterative하게 적용하여 $y_n$을 구한다. 각 시점에서 함수를 선형으로 근사하여 미래의 함숫값을 구하는 방식이다.

\[y_{n+1}=y_{n}+f(x_n, y_n) \Delta x\]

Runge-Kutta Method

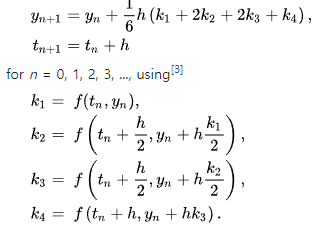
위는 RK4(4개의 항을 이용하는 Runge-Kutta Method)의 수식이며, Euler Method보다 정확하게 수치적분을 할 수 있다.

각 iteration에서 오차는 $O(h^4)$, total accumulated error은 $O(h^5)$라고 한다.

Seperable First-order equation

좌변에 종속변수에 대한 수식, 우변에 독립변수에 대한 수식으로 정리가 되면 Seperable하다고 하고, 특히 first-order seperable equation은 간단한 풀이법이 존재한다.

예를 들어 $y^\prime + y^2\sin{x}=0, y(0)=1$을 보자. 이는 $\frac{1}{y^2}\frac{dy}{dx}=-\sin{x}$로 정리가 되고, 양변을 적분하면 해를 구할 수 있다.

일반화된 해법은 다음과 같다.

\[g(y)\frac{dy}{dx}=f(x), y(x_0)=y_0\]

\[\int_{y_0}^{y} g(y) dy=\int_{x_0}^{x}f(x)dx\]

\[G(y)-G(y_0)=F(x)-F(x_0)\]

(주: 첫번째 줄에서 두번째 줄로 넘어갈 때 양변에 $dx$를 곱해주고 integral을 씌우면 됨)

이제 $x$에 대해 $y$를 정리하면 된다.

Quiz

미분방정식은 예제 문제 풀이가 굉장히 중요하다. 내용 정리에 더해 문제도 꼭 풀어보도록 하자.

y(x)=19(x1/2−1)2\displaystyle{y(x) = \frac{1}{9}(x^{1/2}-1)^2}y(x)=91​(x1/2−1)2 

y(x)=19(x−1)2\displaystyle{y(x) = \frac{1}{9}(x-1)^2}y(x)=91​(x−1)2

y(x)=19(x3/2−1)2\displaystyle{y(x) = \frac{1}{9}(x^{3/2}-1)^2}y(x)=91​(x3/2−1)2

y(x)=19(x2−1)2\displaystyle{y(x) = \frac{1}{9}(x^{2}-1)^2}y(x)=91​(x2−1)2

y(x)=11−ln⁡x\displaystyle{y(x) = \frac{1}{1-\ln{x}}}y(x)=1−lnx1​

y(x)=11−2ln⁡x\displaystyle{y(x) = \frac{1}{1-2\ln{x}}}y(x)=1−2lnx1​

y(x)=11+ln⁡x\displaystyle{y(x) = \frac{1}{1+\ln{x}}}y(x)=1+lnx1​

y(x)=11+2ln⁡x\displaystyle{y(x) = \frac{1}{1+2\ln{x}}}y(x)=1+2lnx1​

y(x)=esin⁡x\displaystyle{y(x) = e^{\sin{x}}}y(x)=esinx

y(x)=ecos⁡x\displaystyle{y(x) = e^{\cos{x}}}y(x)=ecosx

y(x)=e1−sin⁡x\displaystyle{y(x) = e^{1-\sin{x}}}y(x)=e1−sinx

y(x)=e1−cos⁡x\displaystyle{y(x) = e^{1-\cos{x}}}y(x)=e1−cosx

답은 3,1,2

Linear First-order equation

\[\frac{dy}{dx}+p(x)y=q(x), y(x_0)=y_0\]

위 미분방정식을 풀기 위해서, 적분인자(integrating factor) $\mu(x)$을 곱해준다. 그렇다면 적분인자는 뭘까? 양변에 곱해줄 적분인자가 아래 관계식을 만족한다면 적분인자를 양변에 곱한 후 쉽게 정적분이 가능할 것이다.

\[\mu(x)[\frac{dy}{dx}+p(x)y]=\frac{d}{dx}[\mu(x)y]\]

위의 관계를 만족하는 $\mu(x)$는 $\mu(x)p(x)=\frac{\mu(x)}{dx}$에서 $e^{\int_{x_0}^{x} p(x)dx}$라는 것을 알 수 있다. (지수의 integral에서 아래끝은 뭘로 둬도 상관 없지만 편의상 $x_0$로 둔다.)

따라서, 적분인자를 원래의 미분방정식의 양변에 곱하면

\[\mu(x)[\frac{dy}{dx}+p(x)y]=\frac{d}{dx}[\mu(x)y]=\mu(x)q(x)\]

양변을 $x_0$부터 $x$까지 정적분하면

\[\mu(x)y - \mu(x_0)y_0=\int_{x_0}^{x}\mu(x)q(x)dx\]

$\mu(x_0)=1$이고, 위 수식을 정리하면

\[y=\frac{1}{\mu(x)}(\int_{x_0}^{x}\mu(x)q(x)dx+y_0)\]

선형 일계 미분방정식의 해는 위와 같이 결정된다는 사실을 알 수 있다.

Quiz

y(x)=x1+x\displaystyle{y(x) = \frac{x}{1+x}}y(x)=1+xx​

y(x)=x1+x2\displaystyle{y(x) = \frac{x}{1+x^2}}y(x)=1+x2x​

y(x)=x21+x\displaystyle{y(x) = \frac{x^2}{1+x}}y(x)=1+xx2​

y(x)=x21+x2\displaystyle{y(x) = \frac{x^2}{1+x^2}}y(x)=1+x2x2​

y(x)=1+xx\displaystyle{y(x) = \frac{1+x}{x}}y(x)=x1+x​

y(x)=1+xx2\displaystyle{y(x) = \frac{1+x}{x^2}}y(x)=x21+x​

y(x)=1+x2x\displaystyle{y(x) = \frac{1+x^2}{x}}y(x)=x1+x2​

y(x)=1+x2x2\displaystyle{y(x) = \frac{1+x^2}{x^2}}y(x)=x21+x2​

y(x)=a(1−eλx)\displaystyle{y(x) = a(1-e^{\lambda x})}y(x)=a(1−eλx)

y(x)=a(1−e−λx)\displaystyle{y(x) = a(1-e^{-\lambda x})}y(x)=a(1−e−λx)

y(x)=aλ(1−eλx)\displaystyle{y(x) = \frac{a}{\lambda}(1-e^{\lambda x})}y(x)=λa​(1−eλx)

y(x)=aλ(1−e−λx)\displaystyle{y(x) = \frac{a}{\lambda}(1-e^{-\lambda x})}y(x)=λa​(1−e−λx)

답은 4,2,4

* Quiz는 Coursera의 Differential Equations for Engineers에서 따왔습니다.

미분방정식 정리 01 - 미분방정식의 정의, 분류, 수치적 해법, Seperable First-order Equation, Linear First-order Equation

정의

분류

수치적 해법

Euler Method

Runge-Kutta Method

Seperable First-order equation

Quiz

1.

2.

3.

Linear First-order equation

Quiz

1.

2.

3.

미분방정식 Supplementary - Nondimensionalization

미분방정식 정리 02 - 일계선형미분방정식의 응용, Quiz

정의

분류

수치적 해법

Euler Method

Runge-Kutta Method

Seperable First-order equation

Quiz

Linear First-order equation

Quiz

미분방정식 Supplementary - Nondimensionalization

미분방정식 정리 02 - 일계선형미분방정식의 응용, Quiz

You might also like...