미분방정식 정리 07 - Partial Differential Equations
Fourier Series
어떤 함수는 여러 주기함수의 선형결합, 또는 중첩(superposition)으로 나타낼 수 있다.
선형대수 입장에서 서술하자면 함수(벡터)를 여러 주기함수(선형독립인 기저)의 선형결합으로 나타내는 것과 같다.
들어가기 앞서: 함수를 벡터로
함수 $f,g$에 대해 $f+g$가 있으면 $(f+g)(x)=f(x)+g(x)$ 등으로 적절히 논증하면 함수 역시도 벡터로 볼 수 있다는 것을 알 수 있을 것이다.
앞으로 fourier series를 다룰 때 orthogonality, "직교성"을 다룰 텐데, 이러려면 내적(inner product) 공간의 구성과 내적의 정의가 필요하므로 내적을 다음과 같이 정의한다. (주: 벡터 공간과 내적 공간은 똑같은 개념이 아님) $f,g$의 내적은 다음과 같다.
\[\langle f, g\rangle =\frac{1}{P}\int_{x_0}^{x_0+P} f(x) \overline{g(x)} dx\]
이러한 내적의 정의는 실수체, 복소수체에 대해 모두 내적 공간을 잘 형성한다. 복소수체에 대해 내적은 켤체($\overline{g(x)}$)를 활용하는 경우가 잦음을 알아두면 좋다. 이는 보통 양의 정부호성, 즉 자기 자신과 내적했을 때 $(내적값)\ge0$을 만족하기 위해서다.
앞으로의 서술에서 $x_0=-L, P=2L$을 사용한다.
Fourier Series
Frequency $\frac{n \pi}{L}$의 코사인 함수와 사인 함수로 (최대) 주기가 $L$인 함수 $f(x)$를 나타내면 아래와 같다.
\[f(x)=\frac{a_0}{2}+\sum_{n=1}^{\infty} \left(a_n \cos{\frac{n \pi x}{L}} + b_n \sin{\frac{n \pi x}{L}}\right)\]
이러한 코사인 함수들과 사인 함수들은 서로 직교 관계(orthogonality relations)을 만족한다. 앞서 서술한 내적 정의대로 직접 내적해서 확인해보자. 오직 $n=m$일때 $\cos{\frac{n \pi x}{L}}$와 $\cos{\frac{m \pi x}{L}}$, 또는 $\sin{\frac{n \pi x}{L}}$과 $\sin{\frac{m \pi x}{L}}$이 0이 아닌 내적값을 가진다.
\[\langle \cos{\frac{n \pi x}{L}} , \cos{\frac{m \pi x}{L}} \rangle = \frac{\delta_{nm}}{2}\]
\[\langle \sin{\frac{n \pi x}{L}} , \sin{\frac{m \pi x}{L}} \rangle = \frac{\delta_{nm}}{2}\]
\[\langle \cos{\frac{n \pi x}{L}} , \sin{\frac{m \pi x}{L}} \rangle =0\]
그리고 각각의 계수 $a_n$과 $b_n$은, 기저가 직교성(orthogonality)을 만족하므로 $f(x)$에 각각의 기저를 내적하는 것만으로 충분하다.
\[2\langle f, \cos{\frac{n \pi x}{L}} \rangle = \frac{1}{L} \int_{-L}^{L} f(x) \cos{\frac{n \pi x}{L}}dx=a_n\]
\[2\langle f, \sin{\frac{n \pi x}{L}} \rangle = \frac{1}{L} \int_{-L}^{L} f(x) \sin{\frac{n \pi x}{L}}dx=b_n\]
설명을 조금만 덧붙이자면, 물리에서 자주 쓰는 것처럼 3개의 정규직교기저 $\vec{i}, \vec{j}, \vec{k}$를 쓸 때, $\vec{v}$에 $\vec{i}$를 내적하면 $\vec{i}$ 방향 성분이 나오는 것과 똑같다.
Fourier sine and cosine series
특히, $f(x)$가 우함수(even function)일때는 $a_n$과 코사인 함수만을 이용해, 기함수(odd function)일때는 $b_n$과 사인 함수만을 이용해 $f(x)$를 표현할 수 있다.
Fourier Series: Example
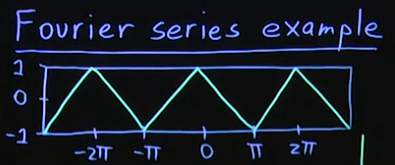
\[f|_{\left[-\pi, \pi\right]}=1-\frac{2}{\pi}|x|\]
위의 $f(x)$에 대해 fourier series로 나타내는 예시를 강의에서 보여주며, 결과는 아래와 같다.
\[f(x)=\frac{8}{\pi^2}\left(\cos{x}+\frac{\cos{3x}}{3^2}+\frac{\cos{5x}}{5^2}+\cdots\right)\]
$x=0$을 대입해 $\frac{\pi^2}{8}=1+\frac{1}{3^2}+\frac{1}{5^2}+\cdots$를 유도할 수 있으며, $A=1+\frac{1}{2^2}+\frac{1}{3^2}+\cdots$로 두면 $\frac{1}{4}A=\frac{1}{2^2}+\frac{1}{4^2}+\cdots$, $A-\frac{1}{4}A=1+\frac{1}{3^2}+\frac{1}{5^2}+\cdots=\frac{\pi^2}{8}$에서 $A=\frac{\pi^2}{6}$이다. (다시 설명하면, 자연수 제곱의 역수 합 : 홀수 제곱 역수 합: 짝수 제곱 역수 합 = 4:3:1임을 이용해 홀수 제곱 역수 합에서 자연수 제곱 역수 합을 구할 수 있다.)
바젤 문제의 해법 중 하나로 참고할 수 있을 듯하다.
Practice Quiz: Fourier Series
답
2,3,2
The Diffusion Equation
유도 과정 쓰기 귀찮으니 결론부터 쓰자면 1차원 상의 확산방정식은 $u_t=Du_{xx}$이다. ($u(x,t)=$ 단위 길이당 질량, 선밀도)
Seperation of Variables
$u(x,t)=X(x)T(t)$와 같이, $u(x,t)$가 $x$와 $t$에 대해 분리된다고 가정하면 종속변수 $X$, $T$에 대한 2개의 미분방정식으로 확산방정식이 찢어진다.
\[\frac{X^{\prime\prime}}{X}=\frac{1}{D}\frac{T^\prime}{T}=-\lambda\]
\[\begin{cases}X^{\prime\prime}+\lambda X=0 \\ T^\prime+\lambda DT=0\end{cases}\]
open pipe ends에 대한 boundary condition $X(0)=X(L)=0$을 이용하면 $u(x,t)$를 아래와 같이 구할 수 있다.
\[X_n= \sin{\frac{n \pi x}{L}}\]
\[T_n(t)=e^{-\frac{n^2\pi^2 Dt}{L^2}}\]
\[u(x,t)=\sum_{n=1}^{\infty}b_n \sin{\frac{n \pi x}{L}}e^{-\frac{n^2\pi^2 Dt}{L^2}}\]
$b_n$ 등의 계수는 앞서 서술했듯 기저랑 내적해서 구하면 된다.
Practice Quiz: Seperation of Variables
답
4,4,3
Practice Quiz: The Diffusion Equation
답
4,1,2
Week Six Assessment
답
3,4,2,2,3,4,1,1,2,3
Farewell
드디어 Differential Equations for Engineers 강의의 정리를 끝마쳤다.
전반적으로 연습문제도 제공해 주는 등 괜찮은 강의였지만... 아쉬운 점이 꽤 많았다.
- 수학적 깊이: 내 정리 글을 보면 알겠지만 선형대수 내용 등이 강의에서 꽤 빠져있어서 내가 따로 덧붙여서 정리했고, 그 외에도 수학적으로 엄밀하게 넘어가야 하는 내용이 너무 많이 빠져 있다는 느낌이 좀 들었다.
- 공학적, 물리적 깊이: 르장드르, 라게르, 베셀 함수 등 충분히 다양한 함수를 다루고 넘어가지 않아 좀 아쉽다.
- 편미분 이후의 미묘한 내용: 편미분방정식 풀이 방법으로 변수분리 외에 소개한 게... 없다. 편미분방정식은 어떻게 풀라는건지 잘 모르겠다.. 원래 다른 미분방정식 강의 들어도 안 알려주나..?
- 과제와 퀴즈의 난이도가 너무 낮다. 어려워도 좀 생각해볼만한 내용 같은 걸 덧붙여줬으면 더 좋지 않았을까 하는 아쉬움이 남는다.



