By MilkClouds in Papers Reading — 2021년 12월 20일

Attention Is All You Need(NIPS 2017)

Google Research의 논문이다.

요약

무려 3만회나 인용된, 가히 혁신적이라고 할 수 있는 논문이다. Attention Mechanism만을 이용한 모델 Transformer을 처음으로 제안하였으며, NLP에 쓰이다 나중에 DETR, ViT, Point Transformer, Perceiver 등 Transformer을 이용한 논문이 수많은 영역에서 우후죽순 생겨나며 간혹 SOTA도 차지하고 있다.

1. Introduction

RNN, LSTM, GRU가 language modeling, machine translation 같은 sequencing modeling과 transduction problems에서 SOTA를 차지해왔다. encoder-decoder arch와 recurrent language models의 경계를 확장하려는 노력도 있어왔다.

Recurrent model의 경우 $h_t$를 $h_{t-1}$에서 계산해 냄으로써 지속적으로 hidden states를 만들어 나가는데, 이러한 sequential nature은 training 도중의 parallelization을 못하도록 한다. 개선 사항이 있었고 improvement of model performance도 있었지만 근본적인 제약은 해결되지 않는다.

3. Model Architecture

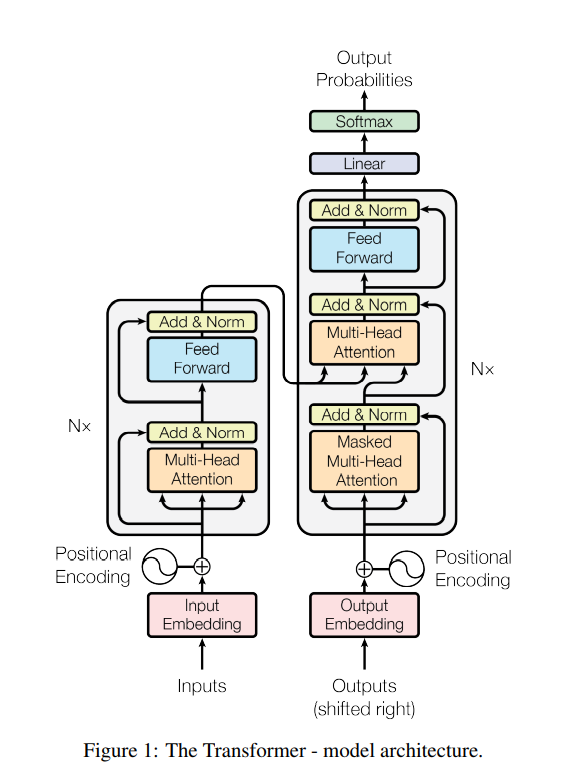
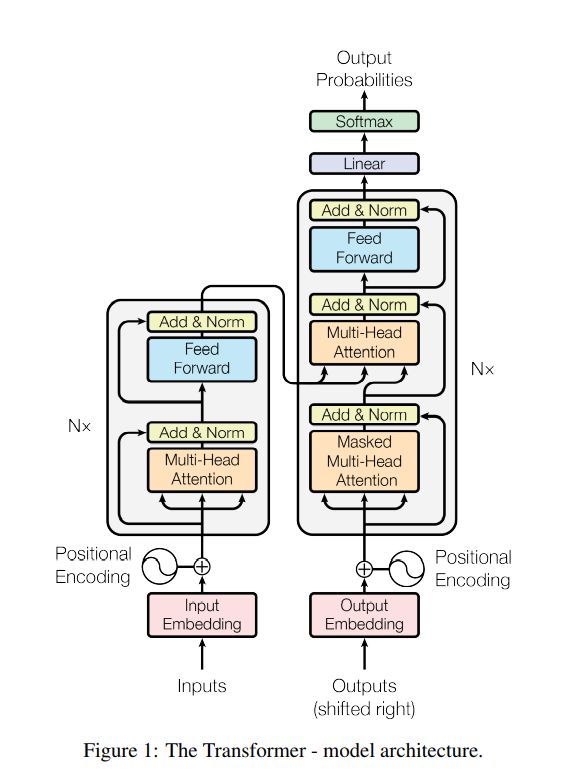
3.1 Encoder and Decoder Stacks

모든 레이어는 skip-connection이 들어간다. (이것을 facilitate하기 위해, 모든 레이어의 output dimension은 $d_{model}=512$로 통일한다.)
skip-connection 직후에는 normalization을 시행한다.
Encoder와 Decoder 구조는 Figure 1을 참고하자. Figure 1만큼 이해가 쉽게 간략하게 만들어 놓은 그림이 없다.
Encoder은 self-attention 후에 feed-forward를 반복한다.
Decoder은 self-attention 후에 encoder의 output을 K, V로 삼은 cross-attention을 하고, 이후 feed-forward를 하는 것을 반복한다.

3.2 Attention

Attention은 Query, Key, Value를 입력으로 받는 연산이다. Query는 영향을 받는 entity, Key(그리고 Value)는 영향을 주는 Entity라고 할 수 있다.

논문 외적으로 첨언하자면, 결국 Q란 내재한, 이미 가지고 있는 정보이며 K,V는 참고할 정보이다. 이것들에 대해 Attention(Q,K,V)를 적용하면 Q에 따라 K를 주목하여 V를 가중합하여, 결과적으로 Q에 K,V의 정보가 적절히 혼합된다.

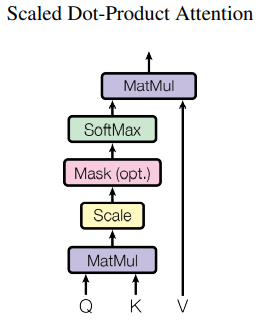
3.2.1 Scaled Dot-Product Attention

먼저 Query와 Key의 유사도를 비교한다. 그리고 이 유사도에 기반해 Value를 가중합한다. 이 유사도를 계산하는 과정에서 내적을 이용한다.

\[Attention(Q,K,V)=softmax({\frac{Q{K^{T}}}{\sqrt{d_{k}}}})V \\ Q=(N,d_k), K=(N,d_k), V=(N, d_v) \]

식을 조금 풀어 설명하자면,

임의의 쿼리 $Q_i \ (0 \le i \lt N)$에 대해 아래 수식이 성립한다.

\[softmax \left( \frac{ Q_i\begin{pmatrix} K_1 \dots K_N \end{pmatrix}} {\sqrt {d_k}} \right) \begin{pmatrix} V_1 \\ \vdots \\ V_N \end{pmatrix}\]

$softmax(\dots)$ 부분은 $Q_i$에 대해 각각의 Key가 얼마나 비슷한지 내적을 이용해 계산한 후 softmax 연산을 적용해 합이 1이 되도록 만든 것이다. 여기다 $V$ 행렬을 곱하면 유사도에 기반한 Value의 가중합이 나올 것이다.

식을 아래와 같이 나타낼 수도 있다.

$$softmax \left( \begin{pmatrix} Q_1 \\ \vdots \\ Q_N \end{pmatrix} \begin{pmatrix} K_1 \dots K_N \end{pmatrix} \bigg/\sqrt{d_k} \right) \begin{pmatrix} V_1 \\ \vdots \\ V_N \end{pmatrix}$$

$\sqrt{d_k}$로 나누는 이유는, $q,k$가 $N(0, 1^2)$를 따르는 독립랜덤변수면 $q \cdot k=\sum^{d_k}_{i=1}q_ik_i$는 $N(0, d_k)$를 따르기 때문이다. $\sqrt{d_k}$로 나눠주며 분산을 1로 만든다. 이렇게 하지 않으면 softmax 함수에서 기울기가 0에 가까운 부분으로 값이 이동하여 gradient가 제대로 전달되지 않을 수 있다.

논문 외적으로 첨언하자면, $Q$의 개수와 $K,V$의 개수는 달라도 된다. (특히 cross-attention에서) 그것을 이용하는 것이 Perceiver: General Perception with Iterative Attention 이다. Q, K, V를 잘 조작하는 논문이 굉장히 많은데 Set Transformer도 그러한 예시이다.

참고로 self-attention이란 Q,K,V가 모두 하나의 출처에서 나왔을 때 쓰는 말이고, cross-attention은 Q의 출처와 K,V의 출처가 다를 때 쓰는 말이다.

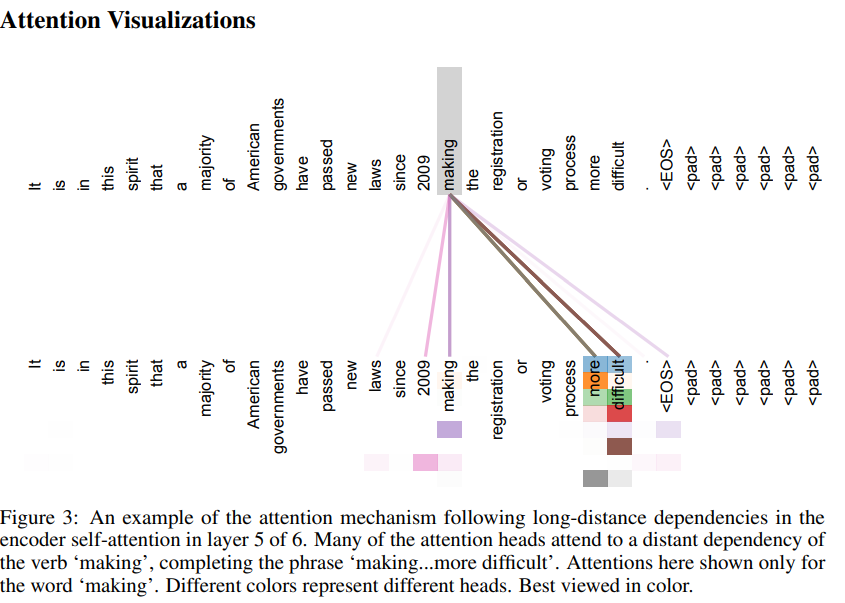
3.2.2 Multi-Head Attention(MHA)

판타지에 나오는 머리가 여럿 달린 생물체가 다방면을 관찰하기 쉬운 것처럼, Transformer에서도 Multi-Head Attention, 즉 attention을 서로 다른 parameter에 대해 여러 번 실행한다. 아래와 같이 하나의 단어에 대해, 각각의 Head가 서로 다른 단어에 주목하게 만들 수 있다. Ensemble의 역할을 해준다고도 볼 수 있겠다.

여러 Head의 결과를 합칠 때는 concat 후 Dense Layer, 단순 행렬곱을 이용한다. V, K, Q에서 Linear layer을 거쳐온 후 여러 head에서 attention을 하고, concat하여 Linear layer로 보내어 결과를 얻는다. 아래 그림에서 V, K, Q는 self-attention의 경우 다 똑같고, cross-attention의 경우 K, V만 다르다고 보면 된다.

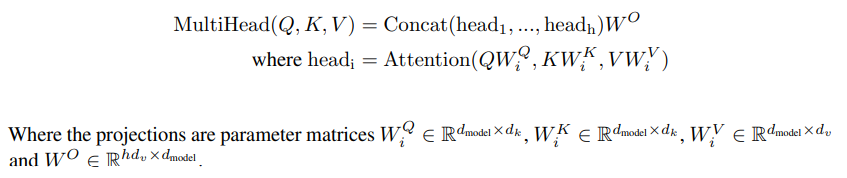
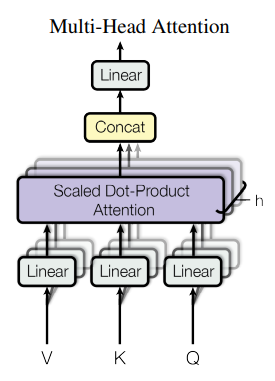
3.2.3 Applications of Attention in our Model

Decoder의 self-attention 도중에는 illegal connections를 제거하기 위해 mask를 쓴다. words가 future word를 참고하지 못하게 하여 information flow를 유효하게 한다고 생각하면 된다. softmax 함수에 들어가기 전 해당하는 행렬 원소를 $-\inf$로 만들어 구현한다.

3.3 Position-wise Feed-Forward Networks

별 거 없고 그냥 pointwise convolution→ReLU→pointwise convolution이다. 각각의 위치($1\dots N$)에 대해 독립적으로 적용되어 feature의 차원만 바꾼다고 생각하면 된다. $d_{model}=512 \rightarrow d_{ff}=2048\rightarrow d_{model}=512$

channel 개수가 늘어났다가 줄어드는 inverted bottleneck 구조이며, 향후 CoAtNet: Marrying Convolution and Attention for All Data Sizes 에서 inverted bottleneck 구조에 주목해 비슷하게 대응되는 MBConv block을 사용한다.

실제로 implementation을 보면 Conv1D로 구현하는 경우가 많으니 참고하자.

3.4 Embeddings and Softmax

기본적으로 NLP에 사용되는 모델이므로(이후 Image Processing등 여러 task에 쓰이지만) 원래의 문장을 embedding으로 바꿔주는 작업을 해야 한다. 또한 이 linear transformation의 weight matrix는 softmax 직전, pre-softmax linear transformation와 weight를 공유한다. embedding layer에서는 $\sqrt{d_{model}}$만큼 곱해준다.

$\sqrt{d_{model}}$만큼 곱해주는 이유에 대해서는, 논문에는 아무 설명이 없고, 1. positional encoding을 더해주기 전 embedding을 충분히 키워주기 위하는 것이라는 설 2. 의미가 없다는 설 3. weight sharing을 해줄 때 고려해야 하는 것이라는 설 이렇게 3가지가 있다. 위 가설 1,2,3에 달아둔 링크 두번째 답변을 보면 word-embedding s.d가 $\frac{1}{\sqrt{d_{model}}}$여서 그렇다는 가설이 가장 신빙성 있어 보인다. PE와 스케일을 맞춰 어느 한쪽이 압도하지 않도록 하는듯.

3.5 Positional Encoding

scaled dot-product attention은 기본적으로 행렬곱 연산이므로 어떤 단어가 몇번째에 있는지에 대한 정보를 처리하지 않는다. 예를 들어 입력 과정에서 항상 첫번째 단어와 마지막 단어를 바꿔서 넣어도 모델의 performance에는 전혀 영향을 주지 않는다. 첫 행과 마지막 행은 사실상 구분이 가지 않기 때문이다.

따라서 각 정보에 위치정보를 더해주기 위해 positional encoding을 더한다. 이는 각각의 위치에 해당하는 sinusoid를 더해줌으로써 해결한다.