[BOJ 18168] Game with Polynomials 2
다항식 $P(x)$에 대해 $(x-x_i)$로 나눈 나머지가 $R(x)$라 하자. 이 때 나머지 정리에 의해 $P(x_i)=R(x_i)$이다.
즉 $P(x_i)$를 계산하는 방법은 직접 계산하는 것 외에, $(x-x_i)$가 포함된 항으로 나눈 나머지 $R(x)$에 $x=x_i$를 대입하는 방법이 있다. 하지만, $(x-x_1), (x-x_2), (x-x_3), \ldots (x-x_Q)$를 각각 하나씩 $P(x)$로 나눠 나머지를 구해 $x=x_i$를 대입하면 그냥 $P(x)$에 $x=x_i$를 대입하는 것과 별반 차이도 없을 뿐더러 나누는 데에 비용도 많이 든다.
다항식의 곱셈과 나눗셈은 FFT를 이용하면 $O(N\log{N})$에 가능하다. $(x-x_i)$로 나눈 정보를 독립적으로 한번만 활용하지 말고, 중첩시켜서 여러번 활용하면 어떨까? 분할 정복을 이용하면 어떨까?
Multipoint Evaluation
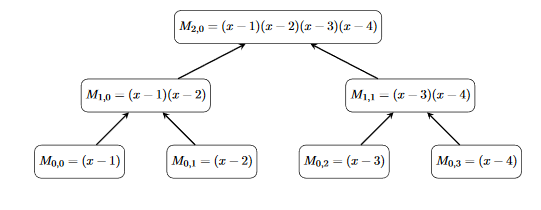
다항식 $f(x)$에 대해 여러 점 $x=x_1, x_2, x_3, \ldots x_Q$에서 $f(x)$의 evaluation 값을 구하는 문제를 multi-point evaluation이라고 한다. 이 문제를 푸는 해법은 다음과 같다.
먼저, query 대상인 각 점 $x=x_1, x_2, \ldots$에 대해 위 그림과 같이 polynomial tree를 구성한다. 전체 트리를 구성하는 비용은 $T(n)=2T(\frac{n}{2})+O(n\log{n})$에서 $O(n\log^2{n})$이다.
트리의 root에서부터 차례대로 $P(x)$를 각 트리의 node에 저장된 다항식 $Q(x)$로 나눈다. 나머지 $R(x)$를 저장해 두고, 트리의 자식으로 내려갈 때 $P(x)$ 대신 $R(x)$를 $Q^\prime(x)$로 나눠 새로운 나머지 $R^\prime(x)$를 구한다.
이 과정을 반복하면 트리의 리프로 내려왔을 때 $(x-x_i)$로 나눈 나머지를 구할 수 있으며(또는 $(x-x_i)(x-x_{i+1})$로 나눈 나머지를 구할 수 있을텐데 이건 그냥 구현에 따라 본질에 별반 차이 없는 사소한 디테일이다), 이렇게 구한 나머지에 $x=x_i$를 대입하면 각 점 $x=x_i$에서 $f(x)$의 evaluation 값을 구할 수 있다.
트리의 root에서 길이 $n$의 다항식을 길이 $q$의 다항식으로 나누는 비용은 $O(n\log{n})$, 트리의 리프로 내려갈 때 길이 $q$의 다항식을 $\frac{q}{2}$ 길이의 다항식으로 2번 나누므로 $T(n)=2T(\frac{n}{2})+O(n\log{n})$이다. $T(n)=O(n\log^2{n})$이며, 이는 트리를 구성하는 데 소모한 비용과 같다.
$N$과 $Q$를 구별해 좀 더 정확히 서술하면 대략 $O(Q\log^2{Q}+N\log{N})$ 정도가 걸릴 것이다.
Solved.ac 기준 Diamond I 문제지만, 풀이를 전혀 모르는 사람이 생각해내긴 어렵겠지만, 풀이를 보면 그닥 어렵지 않고 구현도 어렵지(?) 않다. modint, fft, polynomial 등은 있는 소스코드 가져다 쓰면 되고 나머지 부분은 구현하기 어려운 게 없기 때문이다. 내가 직접 구현하지 않은, 그리고 찾아보면 쉽게 나오는 mint, fft, polymod, segtree를 제외한 소스코드를 첨부한다. segtree는 index $\left[\text{tree.size, tree.size+Q} \right)$가 리프노드고 1-indexed, 루트가 1인 구현본을 사용했다.
poly S(poly& a, poly& b){return a * b;}
poly e(){return poly(1);}
using Seg = segtree<poly, S, e>;
Seg tree;
ll N, Q;
vector<mint> a, b;
void solve(int node, poly& P){
if(tree.size <= node){
if(node < tree.size + Q){
cout << P[0] + P[1] * b[node - tree.size] << "\n";
}
return;
}
poly& Q = tree.d[node];
poly&& R = P % Q;
solve(node * 2, R);
solve(node * 2 + 1, R);
}
int main() {
cin.tie(0) -> sync_with_stdio(false); cout.tie(0);
cin >> N >> Q;
a.resize(N + 1); b.resize(Q);
cinA(a, N + 1); cinA(b, Q);
reverse(all(a));
vector<poly> v;
rep(i, 0, Q){
v.eb(poly({-b[i], 1}));
}
tree = Seg(v);
poly aa = poly(a);
solve(1, aa);
}
추가 참고자료)


