이공계 전반에 걸쳐 정말 많은 분야에서 Boltzmann Distribution 내지 softmax function 등을 사용한다. 하지만 이게 어떤 의미를 가지고 어떻게 유도되었는지, 일단 내가 딥러닝 분야에서 소프트맥스함수를 배우고 한참동안 몰랐다.

하지만 이번 1학기에 통계물리를 가볍게 접하며 이게 도대체 어떻게 유도가 된건지 깨달았고, 그에 대한 내용을 올려보려고 한다.

유도 방법 1

Boltzmann Statistics에서는 모든 입자가 구분 가능하다는 전제 하에, $E_s$의 에너지에 $g_s$의 degeneracy가 존재하고^[1] 입자의 개수가 전체 $N$개라면 $E_s$를 가지는 입자가 $n_s$개일 경우의 수를 아래와 같이 계산한다. 유도 과정은 어렵지 않으니 생략한다. 모르겠다면 Multinomial distribution을 참고하라.
$$\Omega = N! \prod_s \dfrac{g_s^{n_s}}{n_s!}$$
입자의 총 개수 $\sum n_s$가 $N$으로 일정하며, 총 에너지 $E=\sum n_sE_s$가 $U$로 일정하다고 가정하자.
$n$이 충분히 클 때, 스털링 근사에 의해 $\ln{n!} \sim n\ln{n}-n$이고^[2] 확률(경우의 수)를 최대화하기위해 라그랑주 승수법을 사용하면

$$\begin{align}\mathcal{L} &= \ln \Omega+\alpha(N-\sum n_s) + \beta(U - \sum n_s E_s) \\\delta \mathcal{L} &= \sum(\ln g_s -\ln n_s - \alpha - \beta E_s) \delta n_s=0 \end{align}$$

여기서 Boltzmann statistic: $\dfrac{n_s}{g_s} = e^{-\alpha-\beta E_s}$이 유도된다.
즉 $n_s \propto g_s e^{-\beta E_s}$으로 우리가 softmax function에서 보던 꼴이 나왔다. (degeneracy $g_s$를 1로 두었을 때 꼴이 익숙할 것이다.)

물론 $N-\sum n_s$는 $1-\sum \dfrac{n_s}{N}$으로 고칠 수 있으며 $U-\sum n_s E_s$는 $\dfrac{U}{N}-\sum \dfrac{n_s}{N}{E_s}$로 고칠 수 있다. 우리는 입자 개수가 필요한 게 아니라 그 비 율이 필요하기 때문이다.

다시 말해, softmax distribution이란 가능한 에너지 ${E_s}$가 주어지고 입자들이 일정한 평 균 에너지 $\bar{U}=\dfrac{U}{N}$를 가질 때 가장 확률이 큰 분포이다. 확률이 크다는 건 그 상태에 있는 가능성이 가장 높다는 것이고 어떤 의미로 가장 자연스러운 분포라고 할 수 있다.

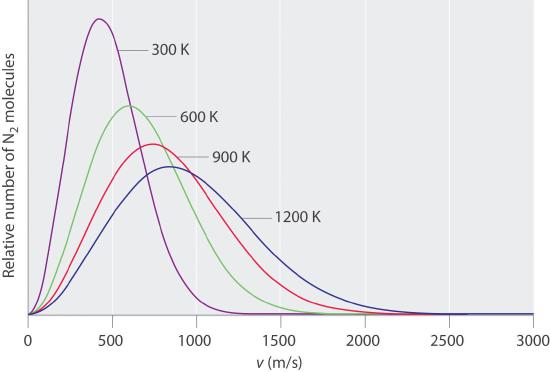
또한, 이 때 $\mathcal{L}$을 총 에너지 $E$로 미분하면 $0=\dfrac{d\ln\Omega}{dE}+\beta(-\dfrac{dE}{dE})$이고 온도의 정의 $\dfrac{d\ln\Omega}{dE}=\beta=\dfrac{1}{kT}$에서 (전자의 $\beta$와 후자의 $\beta$는 수식 유도를 끝마치기 전에는 다르다고 봐야 하나 결과적으로는 같다는 결론이 나온다) $\beta=\dfrac{1}{kT}$이다.  낮은 온도는 입자의 에너지 분포를 왼쪽으로 밀고(저에너지 입자가 많도록), 높은 온도는 입자의 에너지 분포를 오른쪽으로 민다(고에너지 입자가 많도록).

유도 방법 2

https://freshrimpsushi.github.io/posts/boltzmann-distribution/ 을 참고하자.

다만 일반적으로 딥러닝 분야에서 사용되는 softmax 함수가 이러한 물리적 의미를 함의하는 것  같지는 않다. 예를 들어, FC layer의 output으로 $y_1, y_2, \ldots$가 나오면 이들의 softmax  결과를 토대로 여기에 '확률'이라는 개념을 부여해(총합이 1이므로) $\dfrac{e^{y_1}}{\sum e^{y_i}}$의 확률로 label 1이 선택되겠구나~ 이렇게 해석을 한다.

굳이 여기다 물리적인 함의를 끼워맞추자면 음의 에너지 $-y_1, -y_2, \ldots$를 가진 입자들이 있을 때 이들의 평균 에너지를 일정하게 할 때 가장 자연스러운 분포가 softmax distribution이 더라.. 이 정도...?

다만 여기서 의문은 "왜 굳이 실제 에너지도 아닌 것에 대해 평균 에너지를 일정하게 해야 하느 냐?"는 것이고 이게 설명이 안 된다. 굳이 뭔가 다른 자연스러운 설명을 찾자면 차라리 "에너지 를 최소화하자!"가 있을거고 이 경우 그냥 $\text{argmax}_i y_i$를 고르면 된다. 실제로 inference의 경우 어차피 최댓값만 필요하고 softmax 함수는 단조증가 함수이기에 그냥 softmax 돌리지 않고 최댓값 가진 레이블만 뽑아와도 되고.

다만 이렇게 하면 cross-entropy error가 true prediction에 대해 0, false prediction에 대해  무한대가 되어버리므로 training에 크게 쓸모가 없어진다. 물론 이렇게 학습을 하는 실험도 없지는 않겠다만..

softmax 함수를 딥러닝에서 사용하는 것은 그냥 개형 적절히 잘 생겼고, 미분 가능하고, 합이 1 이라 확률로 해석이 가능하고, 립시츠고, 뭐 이 정도...?로 해석할 수 있을 듯하다. 물리적 함의를 끼워맞추려 해도 생각나는 게 없다.

물론, Gumbel-Softmax Trick에서처럼 softmax 함수에 단일한 입력 벡터만을 넣지 않고 온도 파라미터 $\tau$를 넣어주는 경우는 온도의 물리적인 함의를 이용한다고 볼 수 있다.

좀 다르게 잘 해석할 수도 있을 것 같은데, 그런 게 나중에 생각나면 포스트를 업데이트할지도  모른다.