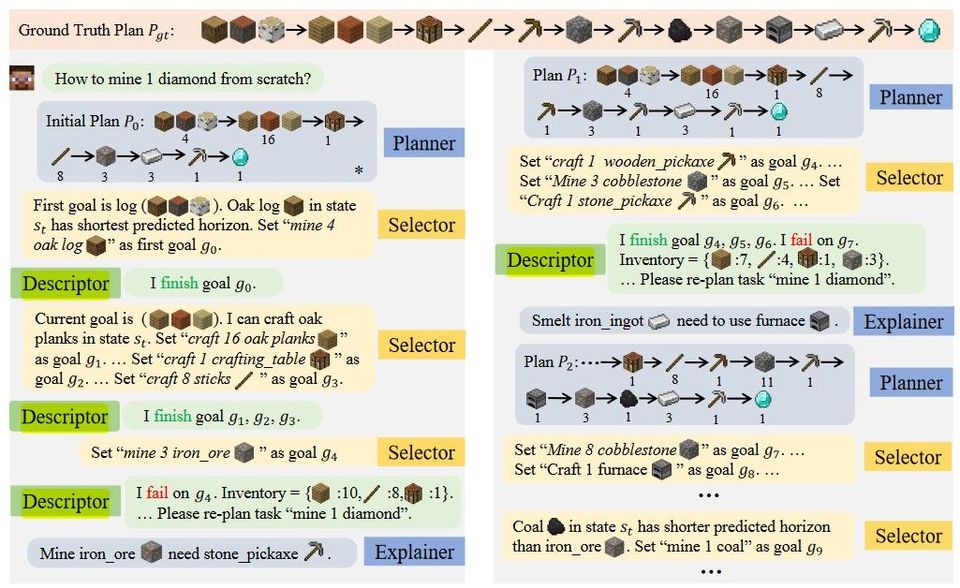
Experimental quantum speed-up in reinforcement learning agents
이 논문에서는 quantum algorithm을 이용해 reinforcement learning을 speed-up하는 것을 실험적으로 보입니다.(quantum-enhanced RL)
이 글은 해당 논문을 간단하게 리뷰합니다.
Summary
이 논문에서는 amplitude amplification을 이용해 reward가 0보다 큰 state의 amplitude를 극대화시켜, quantum-enhanced 된 RL을 합니다. 실제 양자 디바이스 위에서 2 qubit, 2 state, 0/1 reward 환경에서 quantum advantage를 실험적으로 보였습니다.
Prerequisites
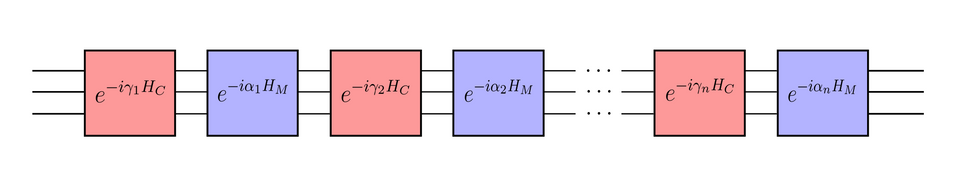
Amplitude amplification을 이미 알고 있다면 더 설명할 게 없다. 간단히만 설명하자면, Grover's Algorithm에서 state preparation unitary를 $H^{\otimes n}$ 대신 다른 유니터리로 바꿔준다.
예를 들어,

위는 https://qiskit.org/documentation/tutorials/algorithms/06_grover.html 에 나온 설명인데 위의 $Q$에서 $\mathcal{A}$를 적당히 바꿔줘서 사용한다는 말이다. 전체 양자회로는 $Q^n \mathcal{A}\ket{0}$와 같이 구성될 것이다.
논문에서 $\mathcal{A}$는 RL에서 얻은 action probability를 거의 그대로 넣어 구현하고, $n=1$로 실험한다.
Brief Review
Reinforcement Learning에서 주요한 요소는 state, action, reward이다. 이러한 $(s, a, r)$ 페어는 quantum state $(\ket{s}, \ket{a}, \ket{r})$로 나타내어 quantum scheme에서 사용할 수 있다.
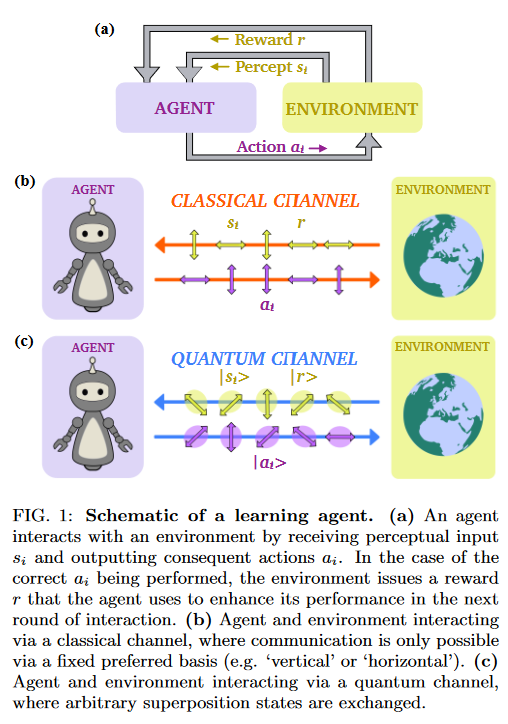
이 논문에서는 quantum-enhanced RL scenario를 고려한다. 위에서 이미 말했듯 state, action, reward를 quantum state로 나타내어 이용하고(quantum channel) 따라서 이들의 중첩 상태 역시도 구축하여 이용할 수 있게 된다.
이 논문에서는 deterministic strictly epochal(DSE) learning scenario만에 집중한다. 이들은 어떤 action $a$에 대해 $s(a), r(a)$가 결정론적으로 정해지는 문제들이다.
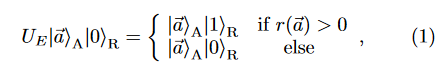
이 논문에서는 풀고자 하는 어떠한 문제에 대한 Oracle $U_E$가 주어져있다고 가정한다. $U_E$는 그로버 알고리즘의 유니터리 자리에 들어가 amplitude amplitifcation에 쓰인다. 저 $U_E$를 그로버 알고리즘의 유니터리로 쓴다는 것의 의미를 설명하자면, 보조 비트인 $\ket{0}_R$에 대해 보조 비트를 $\ket{1}_R$로 만들어주는 state $a$들에 대한 $\ket{a}$만을 '극대화'해주겠다는 의미이다. 다시 말해 reward가 0 초과인 상태의 확률진폭만을 크게 만든다.
이론상 대충 Hadamard 게이트로 균일하게($\sum_x \ket{x}$)로 초기화해두고 저 유니터리 게이트를 이용한 Grover Operator을 반복적으로 적용하면 $\sqrt{N}$만에 답이 나온다. (이 방법 역시도 quantum advantage를 얻을 수 있다.) 그러나 이 논문에서는 Grover iteration은 단 한번만 가해주고, state preparation 과정을 최적화한다.
구체적인 방법은 부록 자리의 Methods에 나와있다.

위와 같이 reward를 고려한 $h(a)$를 정의하고,

- A.7과 같이 state preparation을 한다.
- grover iteration을 가한다. 위의 A.8은 일반적인 $k$를 다루고 있는데, 실험에서는 $k=1$이다.
- grover iteration을 거친 후의 결과를 measure해서 action을 얻는다. (quantum-enhanced action sampling)
- action을 environment에 실제로 취해서 reward를 얻는다.
- 실제로 얻은 reward를 이용해 $h(a)$를 업데이트한다. $h(a)$가 업데이트됨에 따라 당연히 $p(a)$도 업데이트되고 state preparation unitary도 업데이트된다.
Experiments
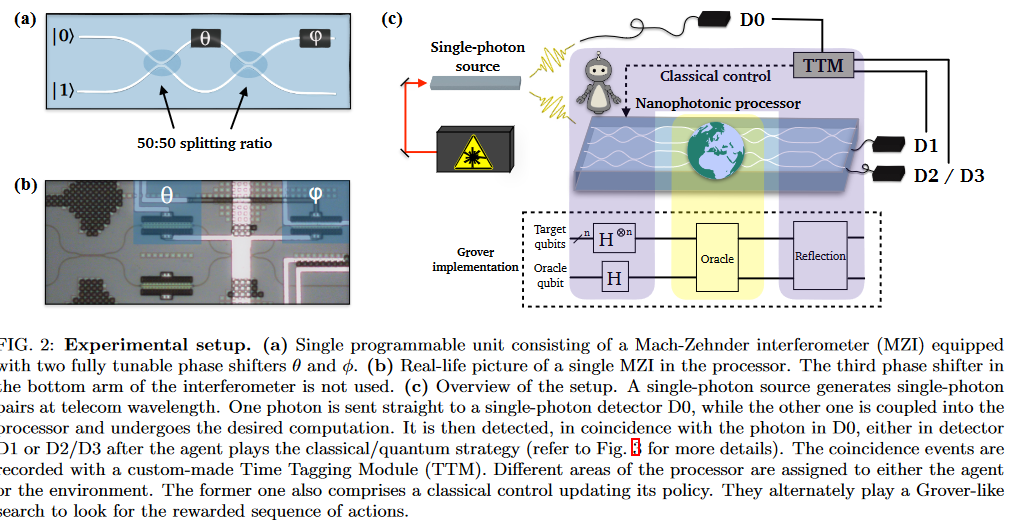

실제 실험은 위와 같은 실험 장치에서 진행한다. 2-qubit, 2-state, 0/1 reward이다. FIG3의 quantum circuit은 위에서 설명한 알고리즘을 그대로 구현한다. ($k=1$)
Results
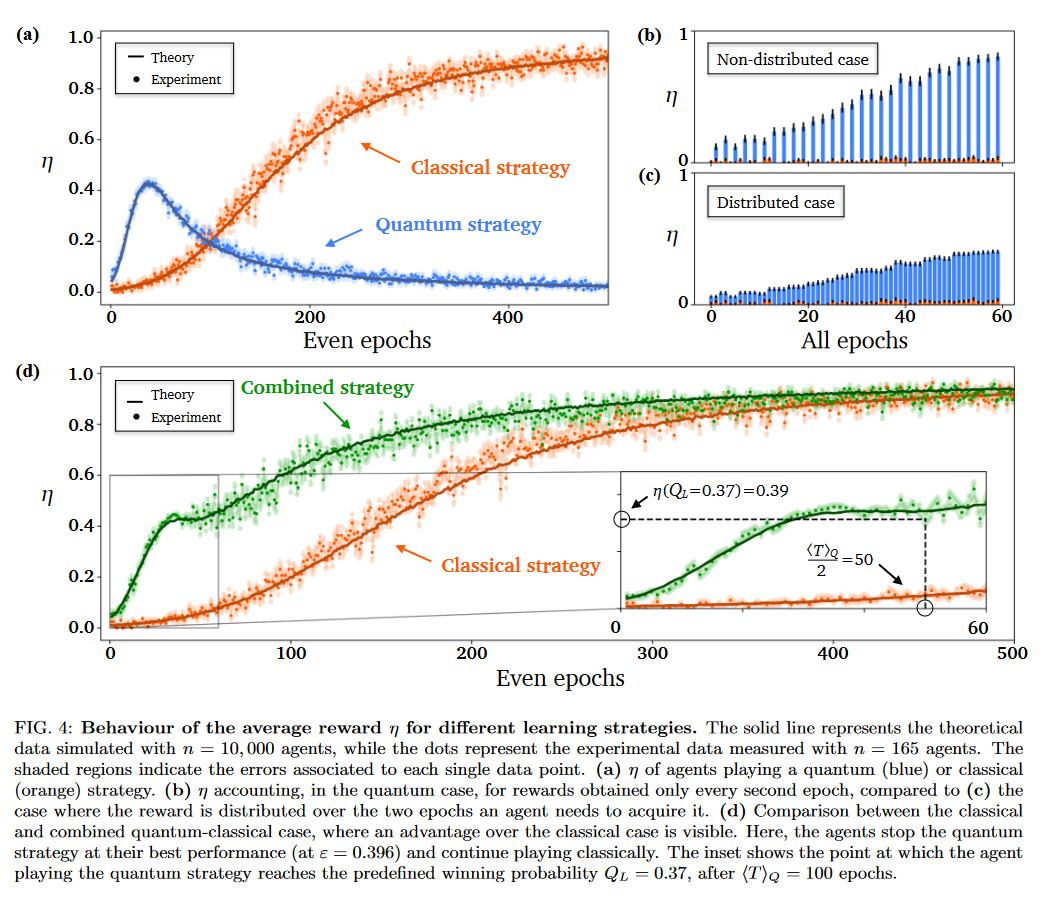
그냥 그로버 알고리즘이 아니라 그로버 닮은 알고리즘이라, 일정 $\sin^2(\xi)=\epsilon$, 특히 $k=1$일 때 $Q:=0.396$ 이후부터는 정답의 확률진폭이 늘어나지 않아 오히려 성능이 감소한다. 그래서 이 역치 전까지 quantum-enhanced, 그 이후로는 classical 방법으로 RL하는 strategy를 'combined strategy'라 한다.
그림 보면 combined strategy가 classical strategy보다 나은 모습이다.
근데 부록의 모든 리워드를 2로 나눠서 그려서 그린 것 같다. Fig4의 (d)에서 확대해서 표기한 $0.37$에서의 리워드도 $0.39$인데 이게 딱 $2\sin^2(\xi), \sin^2(3\xi)$를 반 나누면 나오는 값이다.
이것 외에는 quantum enhanced RL은 한번에 2epoch를 센다는 점도 있다. 뭐 fairly하게 하려고 이렇게 한다고 하는데 납득이 크게 가진 않는다.
Conclusion
RL에서의 quantum advantage를 실험적으로 보인 의미있는 논문이지만 2-qubit, 2 state, 0/1 reward 상황에 대한 실험이었다는 점에서 한계도 굉장히 크다.[1] 논문의 이론적인 부분을 봤을 때도 0/1 reward 외에는 확장이 안된다. 정확히는, reward에 기반해 policy를 계산하는 건 RL로 하기 때문에, 0/1 외에 continuous reward를 사용하는 것이 가능/불가능한지를 따지면 당연히 가능하다. 하지만 Oracle $U_E$가 오직 reward가 0보다 클 때만을 고려하기 때문에 $0$ 이외의 reward를 가지는 state들은 우선순위를 줄 수가 없다. 즉 0/1 reward 이외에, 0 이외의 reward들을 따졌을 때 이들에 대해 quantum advantage를 얻을 수 없다.
이러한 문제의 해결법을 간단히 생각해보자면, $U_E$를 적당히 reward threshold가 점점 높아지도록 구성한다든지, 애초에 threshold를 높인채로 구성한다든지 하는 방법이 있겠다. 뭐 그냥 잠깐 간단히 생각해본 정도지만. 물론 이러면 $U_E$를 구축하기가 조금 더 어려워질 것이다.
하지만 논문의 결과를 더 발전시켜서 scaled-up된 양자컴퓨터 위에서 돌리면 기존의 RL도 더 빠르게 돌릴 수 있다는 것이기에, 한계도 크지만 향후 기대할 수 있는 부분도 큰 논문인 듯하다.
사실 quantum computer가 오류없이 긴 시간 잘 작동한다면 애초에 렇게 할 필요 없이 그냥 Grover iteration을 여러번 돌리면 되는데.. 하는 생각도 계속 든다. ↩︎