https://arxiv.org/abs/2005.08926
https://github.com/patrick-kidger/NeuralCDE
https://www.youtube.com/watch?v=sbcIKugElZ4

NeurIPS20에 실린 논문이다. 논문 1저자가 유튜브 영상도 올려뒀으니(굉장히 잘 정리되어 있다!) 위의 링크의 영상을 참고하면 도움이 될 것이라 생각한다. 이 글은 발표 내용에 (대부분) 기반하되 논문 내용을 덧붙이는 방식으로 서술한다.

Summary

• Time series를 다루는 새로운 방법을 제시한다.
• irregularly sampled partially observed multivariate time series에도 잘 작동한다.
• observation 간에 memory-efficient adjoint backprop을 이용해 학습할 수 있다.
• 이미 존재하는 툴(Neural ODE)을 이용해 바로(straightforward) 구현할 수 있다.
• SoTA

Recap

ODE

• vector field $f:\mathbb{R}^w \rightarrow \mathbb{R}^w$
• solution $z: [0, T] \rightarrow \mathbb{R}^w$
• ODE: $\dfrac{dz}{dt}(t)=f(z(t)), z(0)=z_0$

CDE

• control $X: [0, T] \rightarrow \mathbb{R}^v$
• vector field $f: \mathbb{R}^w \rightarrow \mathbb{R}^{w\times v}$
• response: $z:[0, T] \rightarrow \mathbb{R}^w$
• CDE: $\dfrac{dz}{dt}(t) = f(z(t)) \dfrac{dX}{dt}(t), z(0)=z_0$

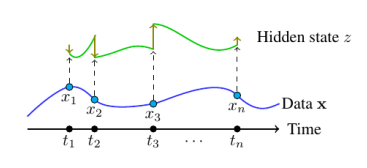
Neural ODE

• Learn a map $x \mapsto y$ by learning a function $f_\theta$ and linear maps $l_\theta^1, l_\theta^2$ s.t.
  • $z(0)=l^1_\theta(x), \dfrac{dz}{dt}(t)=f_\theta(z(t)), y \approx l_\theta^2(z(T))$
  • $z$: hidden state
  • time horizon $T$에 $O(1)$의 memory를 사용하는 효율적인 알고리즘(adjoint backprop)이 존재한다.
  • 

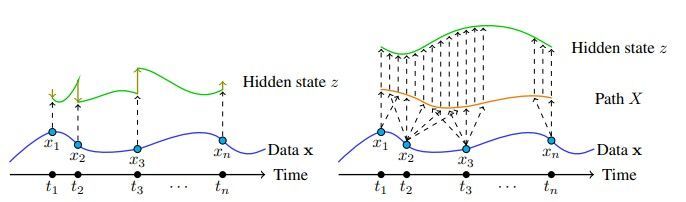
Neural CDE

• 
  • $(t_i, x_i)$를 interpolation한 $X: [0,T]\rightarrow \mathbb{R}^v$의 존재가 NODE와 차이난다.
  • 논문에서 natural cubic spline을 쓴 이유는 이계미분 연속을 보장하기 위해서라고 한다(이계미분이 들어가는 수식이 Appendix A에 있음). Smoothness 말고 이걸 고른 이유는 별 게 없어서, Gaussian processes or kernel methods를 사용해도 된다, noisy data 경우 interpolation scheme 말고 approximation/curve-fitting scheme이 valid하다 언급
• 
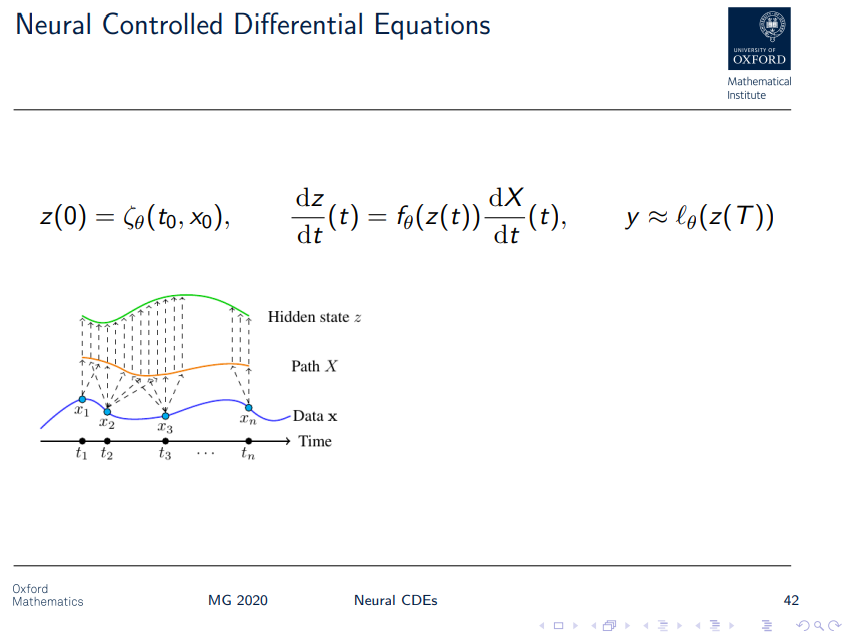
  • Neural ODE와 달리 시계열 데이터를 continuous, $C^2$ path X로 변환한 후 이에 기반해 데이터에 내재된 정보의 변화를 연속적으로 모델링한다.

Advantages

• $\dfrac{dz}{dt}(t) = f(z(t)) \dfrac{dX}{dt}(t)$ 역시 ODE기 때문에 Neural ODE와 같은 툴로 풀 수 있다.
• ODE기 때문에 adjoint backprop을 쓰면 memory-efficient하다.
  • one step evaluation에 cost $H$가 들면 RNN 계열은 $O(HT)$의 메모리를 사용하는 반면 여기서는 $O(H+T)$를 쓴다.
• SoTA

Results

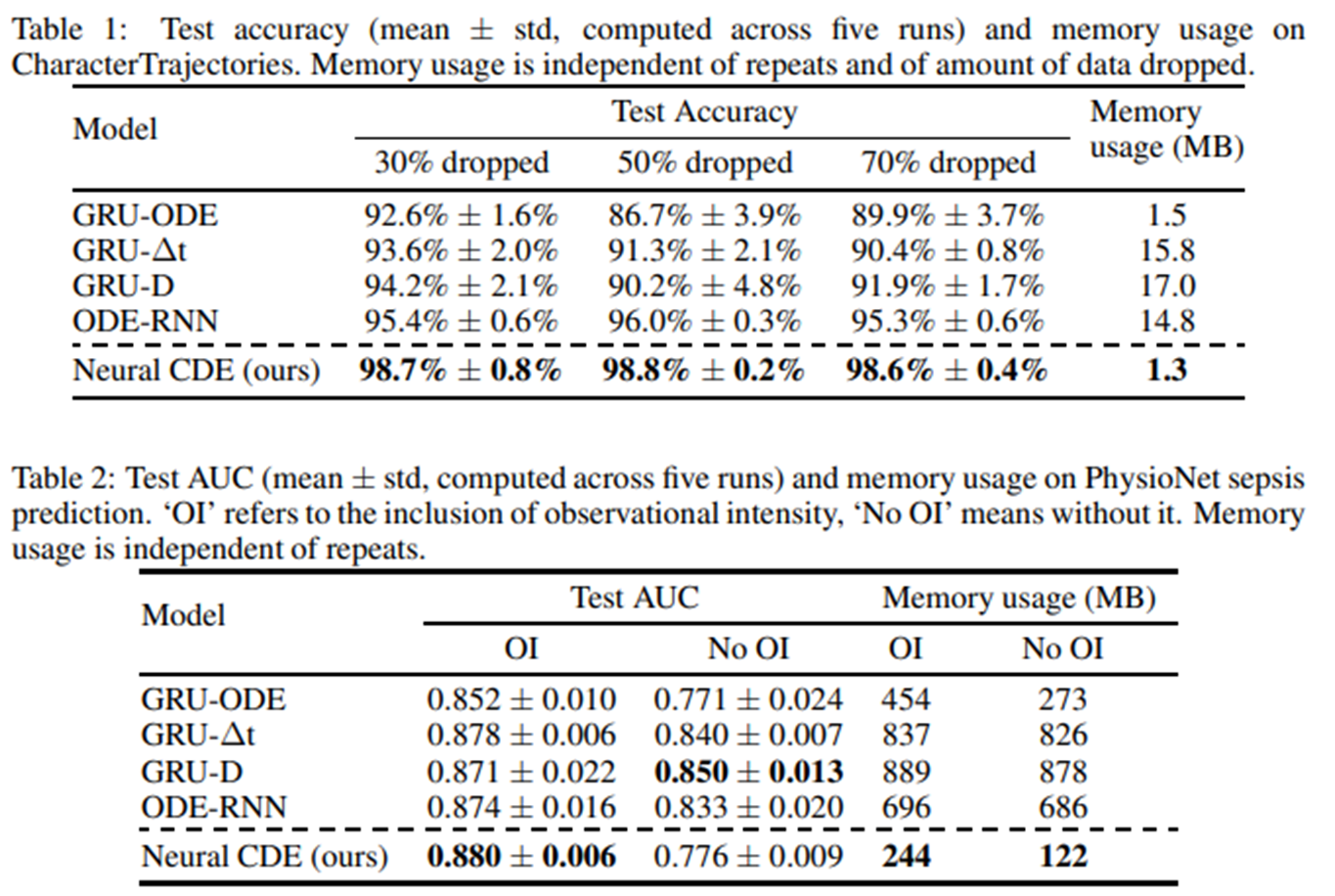
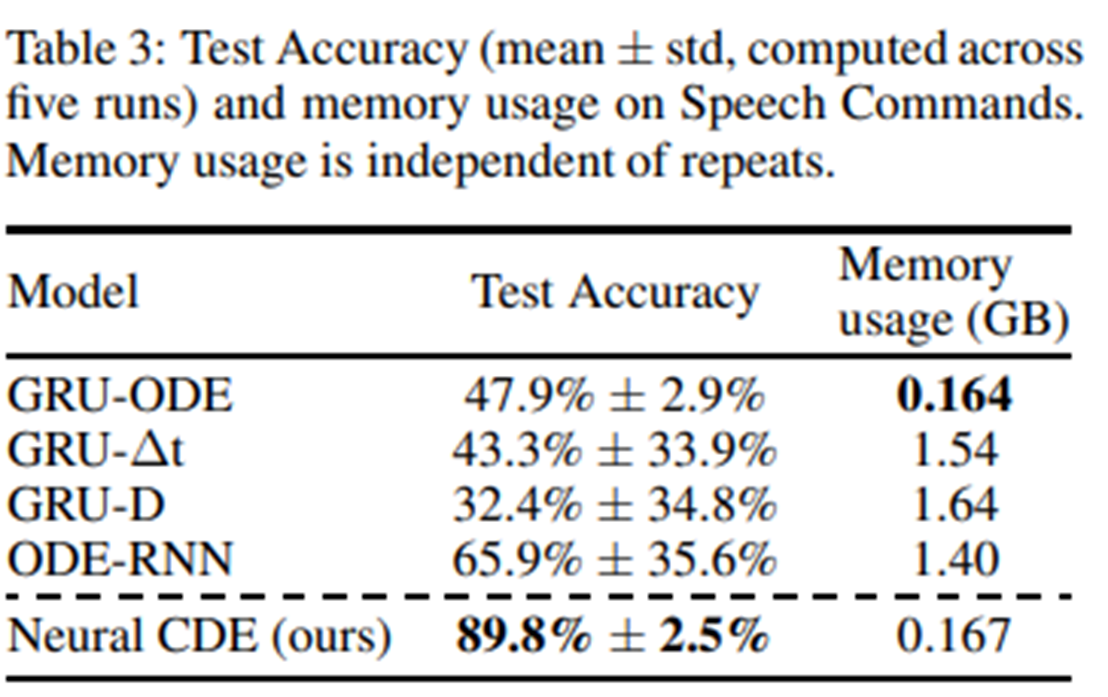
메모리를 적게 사용하며 성능은 상대적으로 높게 나오는 것을 볼 수 있다.
참고로 ODE-RNN, GRU-ODE 등은 RNN과 ODE를 모두 사용하는 모델들이다. 연속적인 변화를 ODE로, 갑작스러운 변화를 RNN으로 모델링한다.