PointNet: Deep Learning on Point Sets for 3D Classification and Segmentation
요약
내가 알기로 Point Cloud를 다루는 시초 격에 해당하는 논문으로, 이후 PointNet++에서 PointNet을 기반으로 개선된 네트워크를 제시한다.
이 논문에서는, permutation invariance에 기반해, 3D voxel grids나 collections of image 없이 point cloud를 직접 다루는 네트워크를 제시한다. Classification, Part Segmentation, Semantic Segmentation에 모두 사용 가능하다.
1줄 요약: $f(x_1,x_2, \ldots x_n)=\gamma(\max _{i=1,\ldots,n}{h(x_i)})$, where $\gamma$ and $h$ for MLP로 permutation invariant하게 output score 뽑아내기. (물론 중간 중간 feature transform을 통해 point간 정보를 섞는다.) global feature은 max pooling 직후에 나온 벡터. function f의 반환값은 x의 permutation에 변하지 않음.
2. Related Work
중간에 Deep Learning on Unordered Sets가 나오는데, 대충 보니 아마도 Seq2Seq에 attention을 적용한 논문을 reference로 제시하는 것 같긴 한데(max pooling 대신 attention sum을 사용한 간단한 실험도 Figure 5에서 제시한다) 이때는 transformer가 유명해지기 전이라 자세히는 제시하지 않은 듯하다. 실제로 최근 어텐션 메커니즘을 이용한 point cloud에 사용하는 네트워크인 Point Transformer도 있으니 관심 있는 사람은 참고하자.
4. Deep Learning on Point Sets
4.1. Properties of Point Sets to $\R^n$
- Unordered. $N!$ permutations
- Interaction among points. neighboring points form meaningful subset. model needs to capture local structures from nearby points
- Invariance under transformation.
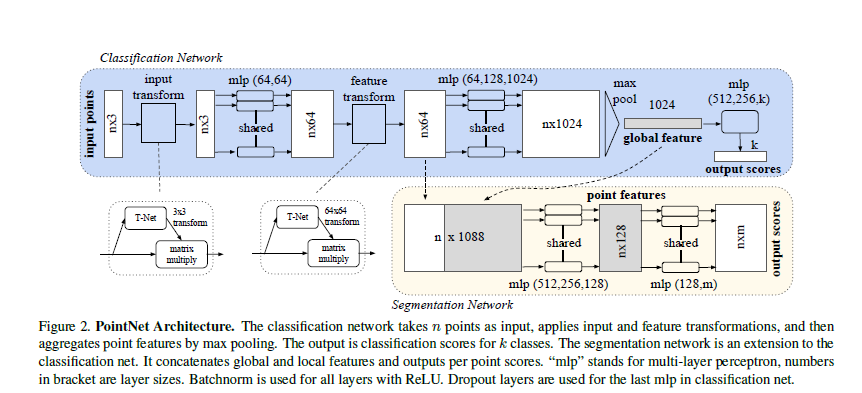
4.2. PointNet Architecture
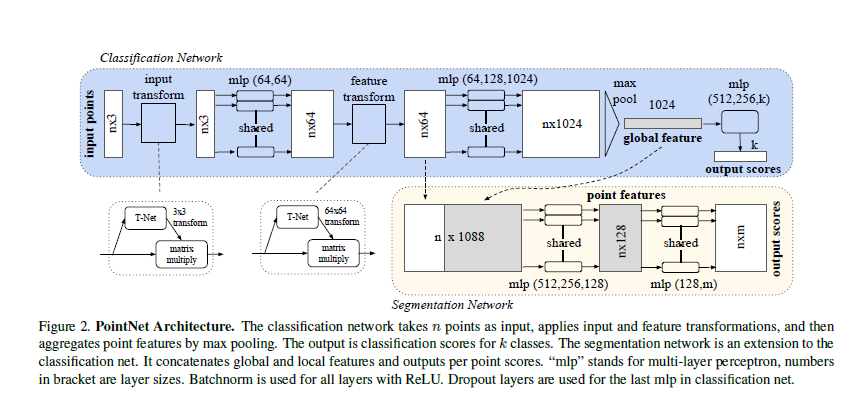
- symmetric function으로 MLP, Max Pooling를 사용.
- global feature
1x1024은 MLP를 거친 후 Max Pooling을 거쳐 추출 - Segmentation에 필요한 local feauture은 local feature과 global feature을 concatenation시켜 만듦. 이후 MLP를 거쳐
n*moutput score을 만든다. - input transform & feature transform: predict affine transformation matrix using deep learning
- 단, feature transform에서 사용하는 64*64 transform은 행렬의 크기가 너무 커 잘 optimization되지 않으므로 orthogonal matrix에 가깝게 만들어주는 regularization term $L_{reg}=|I-AA^T|^2_F$를 추가해준다.
여기에서 shared MLP란, 모든 각 점 1*64에 대해 동일한 64*128 Matrix를 곱하는 레이어를 뜻함.
5.2. Robust함.
5.3. Visualizing PointNet
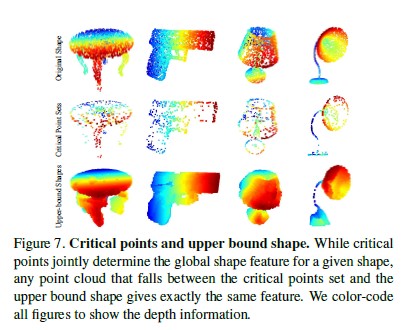
global shape feature에 크게 기여하는 points를 모아 critical points라 하고, 이것을 따로 나타낼 수 있다. 그리고 critical points가 있을 때 global shape를 바꾸지 않는 최대한의 points들을 upper-bound shape라고 한다. critical point sets와 upper-bounded shape는 PointNet의 robustness를 반영한다. non-critical points를 잃는 것은 global shape signature을 바꾸지 않는다는 것을 뜻하기 때문이다.