오늘 조금 놀라운 논문과 실험 결과를 접해서 관련 논문을 리뷰하려고 한다.

PointMLP라는 모델인데, Point Cloud 입력에 대해 residual connection이 존재하는 단순한 MLP(residual MLP)만으로 ModelNet40에서 SOTA인 CurveNet을 뛰어넘어 새로운 SOTA를 달성했다.

좀 특이한 건 저자가 익명이다. ConvMixer도 그렇고 익명 논문이 많은데 무슨 영문인지 모르겠다. 저렇게 써둬도 알만한 사람은 다 알 것 같기도..

Abstract

기존의 연구들에서는 convolution, graph, attention mechanism을 이용해 복잡한 local geometric extractor을 만들었다. 그러나 이러한 방법들은 inference 과정 상당히 느렸고, 그 성능이 어느 정도 포화된 상태이다. 이 논문에서는 local geometrical information을 뽑아내는 것이 핵심이 아니라 판단해 pure residual MLP network, PointMLP를 제시한다.

PointMLP는 딱히 local geometrical extractor이 존재하지 않지만 매우 빠르고, 정확도도 높게 작동한다. 이 논문에서 제시한 가벼운 geometric affine module을 달면 정확도가 더욱 올라가, 실제 세계 기반의 3D 데이터셋인 ScanObjectNN에서는 SOTA를 무려 3.3% 압도했다. 가장 최근의 SOTA인 CurveNet과 비교해 PointMLP는 2배 빠르게 훈련되고 7배 빠르게 테스트되었다고 한다.

1. Introduction

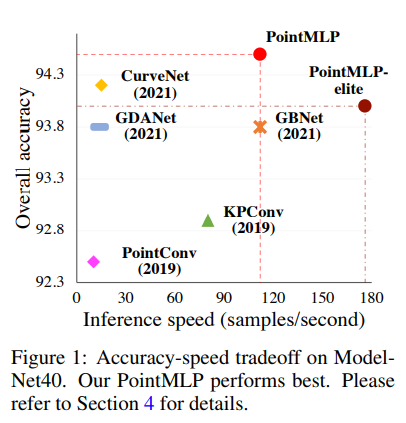
이 논문에서는 residual MLP를 Point Cloud에 적용하고, 또한 성능과 일반화 능력을 키우기 위한 geometric affine module 역시 소개한다.

3. Deep Residual MLP for Point Cloud

기존의 가장 유명한 연구인 PointNet++에서는 FPS(Farthest Point Sampling) 알고리즘을 이용해 $N_s$개의 점을 샘플링하고 각 점에 대해 $K$-neighbors에 대해 feature을 aggregate한다. PointNet++의 kernel operation을 수식으로 나타내면 아래와 같다.

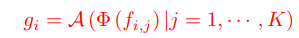
A는 aggregation function(PointNet++에서는 max-pooling), $\phi$는 local feature extraction function(PointNet++에서는 MLP), $f_{i,j}$는 $i$번째 점의 $j$-th neighbor를 말한다.

이러한 설계를 가진 PointNet++은, 효과적으로 지역적인 기하 정보를 추출해낼 수 있었고, 연산을 반복함으로써 receptive field를 키울 수 있었다.

PointNet++은 이전까지 point cloud analysis에 있어 거의 universal한 pipeline이었다. local feature을 추출해내는 데에 있어서는 convolution, graph, self-attention 등의 방법이 쓰였고, 특히 RSCNN은 extractor을 아래와 같이 만들었다.

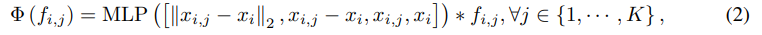
인접한 점까지의 거리, 인접 점까지의 거리벡터, 인접 점의 위치, 자신의 위치를 입력으로 삼아 MLP(FC, BN, activation function을 포함한 작은 네트워크)를 돌리고 feature을 합성곱했다는 말이다.

이에 반해 Point Transformer에서는 아래와 같이 vector 기반의 self-attention을 정의하고, 사용한다.

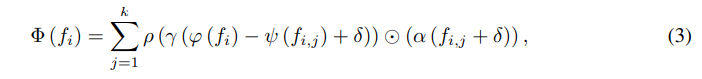
Point Transformer에 대해 간략하게 리뷰한 내 블로그 글도 있긴 하지만, 간략하게 설명하자면 어떤 점에서 인접한 점에 대해 feature을 linear mapping($\varphi, \psi$)한 후, vector substraction 연산을 하고 positional encoding($\delta=\theta(x_i-x_{i,j})$)을 더하고, linear mapping해서($\gamma$), softmax($\rho$)를 취하고, $\alpha(f_{i,j}+\delta)$($\alpha$는 linear mapping)과 성분별 곱(hadamard product)을 해서 더했다는 말이다.

potisional encoding에 쓰인 $\theta$는 2개의, ReLU를 포함한 FC layer이고, 이 간단한 positional encoding의 사용은 Point Transformer의 성능을 크게 향상시켰다.

이러한 방법들이 상세한 지역적 기하 정보의 이점을 쉽게 얻고 어느 정도의 결과를 내긴 했지만, 2개의 이슈가 발전을 막았다. 첫째로, 섬세한 extractor을 사용하면 computational cost가 크게 증가했고 이는 느린 inference latency로 이어졌다. 예를 들어 Point Transformer의 FLOPs는 $14Kd^2$(이조차 summation and substraction operation을 무시한 수치)이고, 고전적 FC layer의 $2Kd^2$보다 훨씬 크다. (memory access cost도 고려되지 않았다) 둘째로 이러한 local feature extractor의 발전에 따른 성능 향상은 거의 포화되기 시작했다. 실제로 Lit et al. (2020)의 실증 조사에 따르면 대부분의 복잡한 local extractor은 같은 네트워크 입력에 대해 거의 같은 성능 향상에 기여했다. 그래서 이 논문에서는 복잡한 local feature extractor을 설계해, 상세한 지역적 기하 정보를 얻어오는 데에 집중하지 않았다.

* 이 논문 흐름과는 관계 없지만 PointNet++을 그대로 가져와 Backbone으로 삼아 여러 종류의 Head를 연결한 네트워크도 몇 있었고, 내가 아는 예시는 Group Free 3D이다. 3D ML 모델에는 Backbone(많은 경우 PointNet++)->Voting->Object Detection based on Vote의 과정을 거치는 네트워크가 꽤 있는데, voting의 개념을 모르는 사람은 VoteNet에 대해 먼저 찾아보자.)

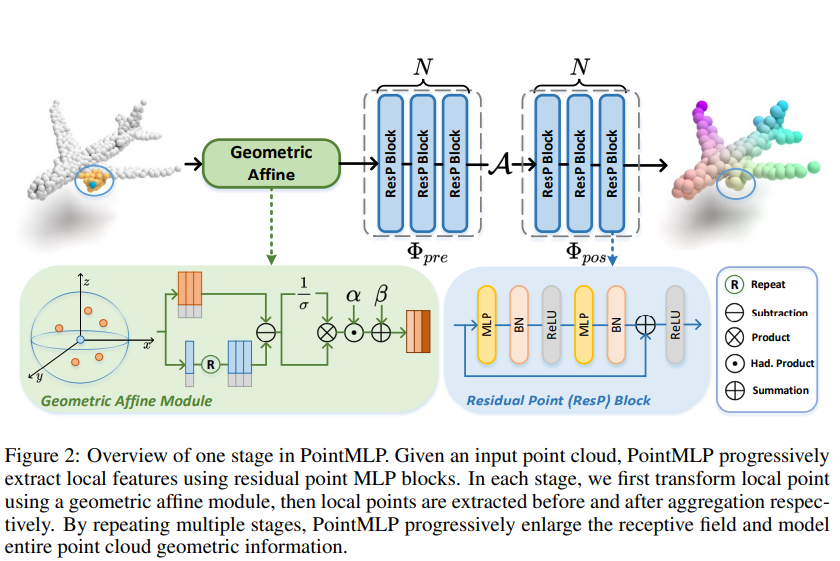
3.2 Framework of PointMLP

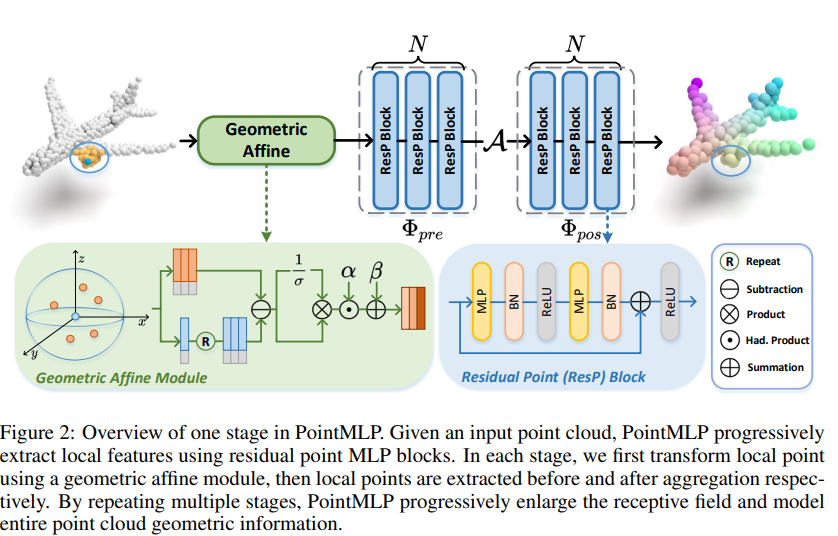
그래서, PointMLP에서는 위의 Figure 2와 같은 간단한 Residual Point Block을 조합해 아래의 연산을 단위 연산으로 삼는다.

\[g_i=\Phi_{pos}(\mathcal{A}(\Phi_{pre}(f_{i,j}, |j=1,\cdots,K))\]

(참고로 논문에 $\Phi_{pre}$ 등이 shared라고 말하는데 별 건 아니고 모든 점 $i$에 하는 연산이 같다는 걸 뜻하는듯)

$\Phi_{pre}$는 aggregation $\mathcal{A}$ 이전의 사전 연산, $\Phi_{pos}$는 aggregation 이후의 사후 연산이라 생각하면 된다. aggregation 연산은 max pooling을 썼다고 한다. 위와 같이 연산을 설계했을 때의 이점을 3개와 같은데-

1. MLP만을 사용하므로 permutation invariant하다. (point cloud 입력에 거의 필수적인 조건)
2. residual connection을 사용하기에 DNN 설계에 유리하다.
3. 복잡한 extractor이 존재하지 않고 highly optimized feed-forward MLP만을 이용하기에 레이어 수가 많아져도 효율적으로 작동한다.

3.3 Geometric Affine Module

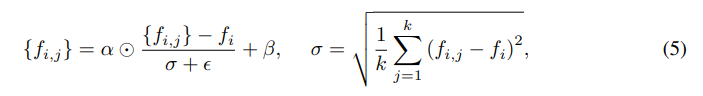
다른 local region에 존재하는 다양한 기하적 구조에 대해 shared residual MLP, 하나의 feature extractor은 작동이 어려울 수 있다. 따라서, $\{f_{i,j}\}_{j=1,\cdots,K}$에 대해 위와 같이 정규화 연산을 해 보편적으로, 안정적으로 학습이 이루어지도록 한다.

3.4 Computational Complexity and Elite Version

FC layer가 highly optimized된 거에 비해, 파라미터 수와 계산 복잡도는 아직 높다. 이것을 개선하기 위해 이 논문에서는 PointMLP의 lightweight version인 pointMLP-elite를 제시한다. (0.7M 이하의 파라미터)

또한 bottleneck 구조를 채용해 파라미터 수를 줄이고 feature extraction에 도움을 준다. (bottleneck 상수 $r=4$) Grouped FC도 시도해봤지만 크게 성능을 손상시켰다고 한다.

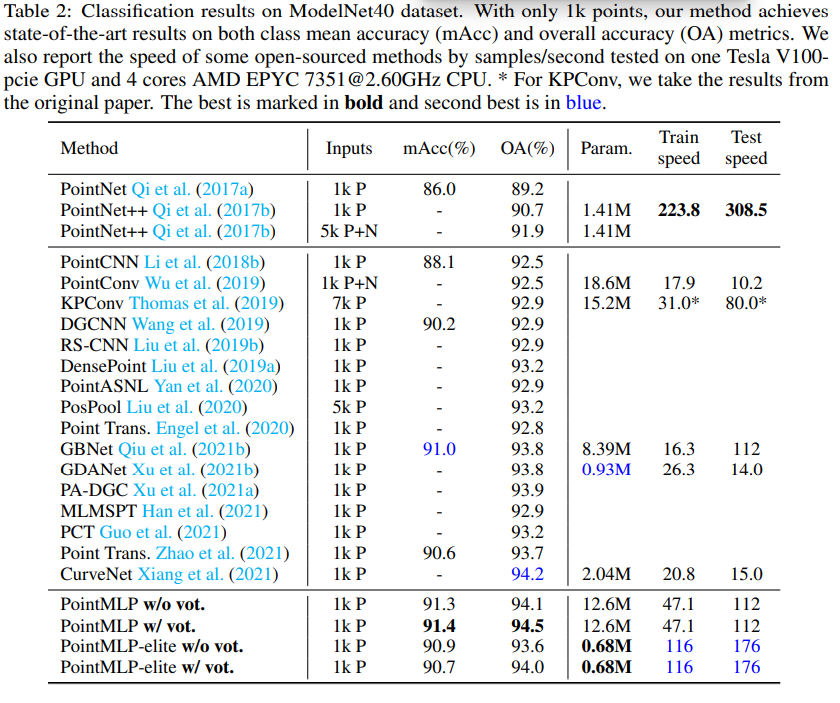
ModelNet40에 대한 파라미터 수, train/test speed, perfomance는 위의 표 참고.

4. Experiments

ModelNet40(합성 3D 데이터셋), ScanObjectNN(실제 3D 데이터셋), ShapeNetPart에 대해 실험을 진행하였다. 앞의 둘 모두에서 SOTA였고, inference speed도 훨씬 빨랐다. 게다가 class mean accuracy와 overall accuracy 사이 gap도 가장 작아, PointMLP가 특정 카테고리에 bias를 가지지 않고 상당한 robustness를 가진다고 할 수 있다.

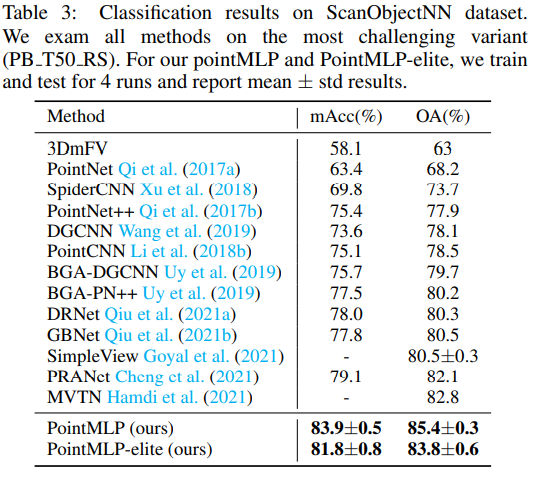
4.3 Ablation Studies

층이 무조건 깊어지게만 설계해도 정확도가 쭉 올라가진 않았고, 다만 표준편차는 예상대로 내려갔다. 40 layer로 설계했을 때 mAcc, OA가 최대였다.

$\Phi_{pre}, \Phi_{pos}$, Affine Module을 지우는 시도를 각각 해봤는데, Affine module을 지웠을 때 정확도가 크게 떨어지며, affine module이 정확도 향상이 크게 기여한다는 것을 알 수 있다.

pre와 pos의 차이는 가장 처음, 입력 데이터가 aggregate 되기 전 처리하는 레이어가 하나라도 존재하는 것과 아닌 것의 차이인걸까? 차이가 꽤 커서 이것도 이유가 궁금하다.

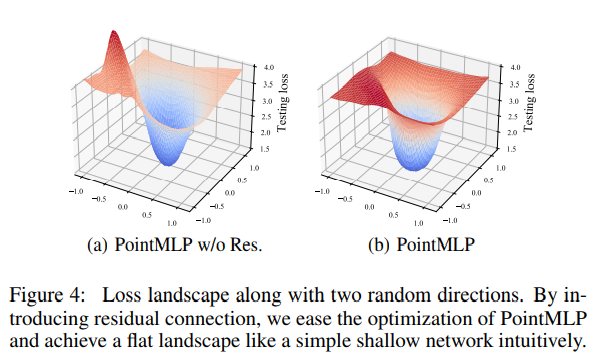
또 residual이 없을 때도 ModelNEt40에서 6% drop이 일어나고 Loss Landscape가 덜 평탄해지는 걸 보여준다.

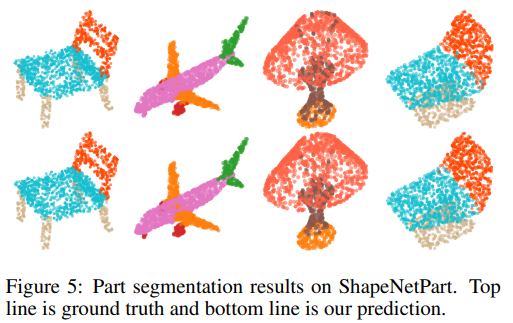
4.4 Part Segmentation

ShapeNetPart에 대해서도 실험 결과를 보여준다.

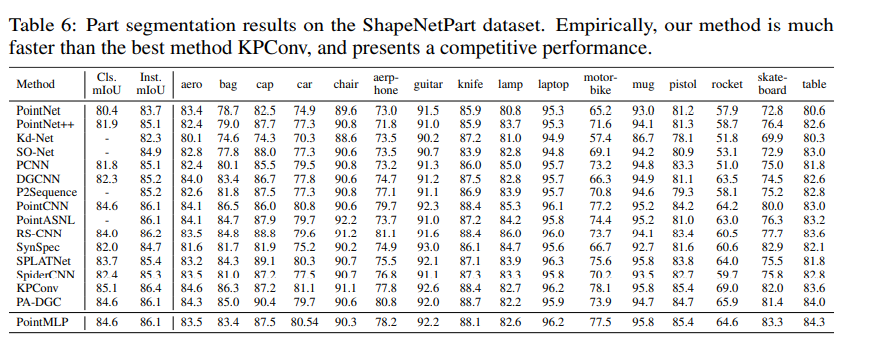
5. Conclusion

이 논문에서는 간단한 residual MLP와 affine module만을 이용해 SOTA를 달성한 PointMLP를 소개한다. 성능이 좋을 뿐만 아니라 inference speed 역시 굉장히 빠른데, 심지어 PointMLP는 응용의 여지도 굉장히 크다는 점에서 기대할 점이 많다고 생각한다.

VoteNet 구조와의 결합, 적절한 변형 등이 앞으로 연구로 나오지 않을까 싶다.

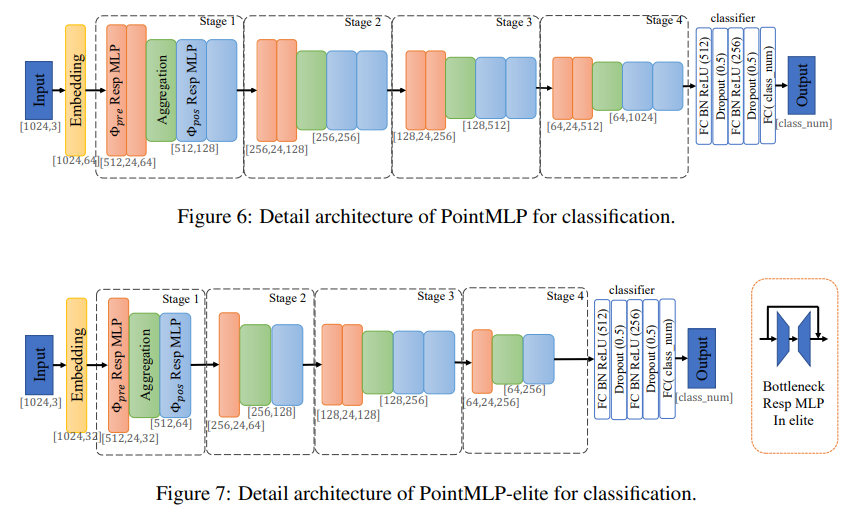
A. PointMLP Detail