이 글은 David Silver의 2015년 Reinforcement Learning 강의를 내 방식으로 일부 재해석해가며 적는 요약 글이다. 이 글 하나만 보고 RL을 처음 배우기는 적합하지 않을 것이며, Sutton의 An Introduction to Reinforcement Learning(한국 번역서: 단단한 강화학습)이나 유튜브 강의를 보며 참고하기를 권장한다. 물론 이미 RL에 대한 기반 지식이 있는데 기억이 희미해지거나 해서 참고하려는 사람은 문제 없을 것이다.

https://www.davidsilver.uk/teaching/

들어가기에 앞서, 표기법은 David Silver의 Lecture에 나온대로, 대부분 Sutton 저서의 내용을 따른다. 표기법에 대해 헷갈리는 게 있다면 sutton의 저서를 참고하자. 예를 들어 $\mathbb{1}$은 indicator function, $$가 붙은 함수는 optimal, $\mathcal{A}$와 같은 curly alphabet은 집합, $V_t$는 $v_\pi$ 또는 $v_$의 추정값, 이런 게 있다.

특히 $V_t$가 $v_\pi$의 추정값임은 잊어버리지 말자.. 내가 이걸 몰라서 헷갈렸었다.

벡터는 본래 bold체로 표기하는 것이 관례상 일반적이나 weight parameter $w$등은 obsidian.md 특성상 왜인지 \bold가 안 먹히고 혼동의 여지가 적으므로 볼드 표시는 생략했다.

---

Lecture 1: Introduction to Reinforcement Learning

Textbook: 단단한 강화학습(An Introduction to Reinforcement Learning), Sutton and Barto

• Agent: observation에 기반하여 action을 하고 그에 상응한 reward를 받아 decision을 수정해 나가는 주체
• Environment: Agent 외부의 환경

몇 가지 기호 표기를 먼저 소개한다. 시간 $t$에서,
action $A_t$, observation $O_t$, scalar reward $R_t$
History $H_t= (O_1, R_1, A_1, \ldots)$
state $S_t = f(H_t)$ (function of history). state에 대한 agent의 표현: $S^a_t$

실제 환경의 상태 $S_t$는 문제에 따라 visible할 수도, 아닐 수도 있다.

Markov state

상태 $S_t$는 $P[S_{t+1}|S_t] = P[S_{t+1}|S_1, \ldots S_t]$, 즉 $S_t$가 현재 시점에 대해 빠짐 없이 충분한 정보를 가지고 있을 때(또는 그러한 가정이 성립할 때) Markov라다고 말한다.

markov state에 대해 과거/현재/미래의 3분류에서, 미래의 예측에는 현재의 state만이 필요하다고 말할 수 있다. environment state $S_t^e$는 Markov하고 history $H_t$는 Markov이다.

Full observability

$$O_t = S_t^a = S_t^e$$
Agent가 environment를 직접적으로 관측할 때

이 때 결정 과정을 Markov decision process(MDP)라고 한다.

Partial observability

agent state $\ne$ environment state (대부분의 문제)
Partially observable Markov decision process(POMDP)

이 때 $S^a_t$는 complete history $H_t$를 쓸 수도 있고 적절한 environment state에 대한 추정량 $\hat{S}_t^a$를 사용할 수도 있다. (neural network 등을 이용해 추정)

Major Components of an RL Agent

Agent의 구성 요소

• Policy: agent's behavior function $\pi(s)$ or $\pi(a|s)$ (deterministic, stochastic)
• Value Function: $v_\pi(s)=\mathbb{E}\pi(R{t+1} +\gamma R_{t+2}+\ldots|S_t=s)$. 미래에 얻을 보상에 대한 기댓값
  이 때 $\gamma$는 어느 분야에서든 흔히 볼 만한 discount factor(할인율)
  돈의 가치가 시간의 흐름에 따라 떨어지는 것(지금 당장 가진 돈의 가치가 높음)과 같이 해석 가능
• Model: 환경에 대한 추정(원 슬라이드에서는 representation이라 언급)

Model의 경우 Model 없는(Model-Free) RL 방법론도 있고 Model이 있는(Model-Based) RL 방법론도 있다. Value, Policy는 둘 중 최소 하나는 있다.

전이 행렬 $\mathcal{P}_{ss'}^a$ : state s에서 action a를 했을 때 state $s'$로 전이할 확률

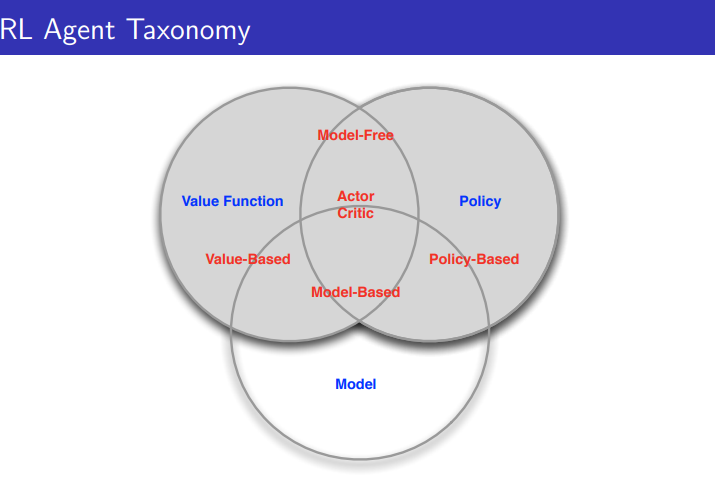
Categorizing RL agents

• Value Based
  • No Policy(Implicit)
  • Value Function
• Policy Based
  • Policy
  • No Value Function
• Actor Critic
  • Policy
  • Value Function

또는

• Model Free
  • Policy and/or Value Function
  • No Model
• Model Based
  • Policy and/or Value Function
  • Model

Learning and Planning

Reinforcement Learning: 환경을 처음 몰랐더라도, 환경과 상호작용하며 policy를 개선해 나간다.
Planning: 환경에 대해 알고 있어 agent는 model에 기반해(외부 상호작용 없이) 연산하며 policy를 개선해 나간다.

Exploration and Exploitation: 전자는 env에 대한 더 많은 정보를 찾고, 후자는 reward를 최대화하기 위해 알고 있는 정보를 exploit한다.

Prediction and Control: 전자는 미래를 예측하고 후자는 미래를 최적화한다. (Find the best policy)

Lecture 2: MDP

MDP는 env가 fully observable할 때를 다루는 것으로 RL을 배울 때 가장 기본적으로 배운다. 거의 모든 RL 문제가 MDP로 formalise될 수 있다.

강의에서 다루는 state, action 등은 모두 유한하다.

Markov Process: $\langle \mathcal{S, P} \rangle$
Markov Reward Process(MRP): $\langle \mathcal{S, P, R, \gamma} \rangle$

MRP을 풀어내기 위해서는 가치 $v$만을 계산해내면 된다.
Bellman Equation: $v=\mathcal{R}+\gamma \mathcal{P}v$
Bellman Equation은 선형 방정식이므로 $v=(I-\gamma P)^{-1} \mathcal{R}$로 바로 풀 수는 있지만 역행렬 계산이 필요하기에 시간 복잡도가 $O(n^3)$ 정도로 large MDP에 대해 실행 불가능하다. large MDP에 대해 Dynamic Programing, Monte-Carlo evaluation, Temporal-Difference learning 등 iterative method를 사용한다.

Markov Decision Process(MDP): $\langle \mathcal{S, A, P, R, \gamma} \rangle$
policy $\pi(a,s)=P(A_t=a|S_t=s)$로 두었을 때 Bellman Expectation Equation $v_\pi=R^\pi+\gamma P^\pi v_\pi$

optimal state-value function: $v_(s)=\max_\pi v_\pi(s)$
optimal action-value function: $q_(s,a)=\max_\pi q_\pi(s,a)$
optimal value function을 알고 있을 때 MDP가 "풀렸다"고 한다.

partial ordering of policy: $\pi \ge \pi'$ if $v_\pi(s)\ge v_{\pi'}(s), \forall s$
there exist optimal policy $\pi_$ s.t $\pi_ \ge \pi, \forall \pi$
optimal policy는 optimal value function과 optimal action-value function을 모두 달성한다. 또한 s,a에 따른 value를 최대화하는 행동만을 고르므로 $\pi_*(a|s)$는 0 또는 1만 나타난다.

$$v_\pi(s)=\sum_{a \in A} \pi(a|s) q_\pi(s,a)$$
$$q_\pi(s,a)=R^a_s+\gamma \sum_{s' \in S}P^{a}{ss'}v\pi(s')$$
위 두 방정식을 엮어서 Bellman Optimality Equation을 나타내면
$$v_(s)= \max_a R^a_s+\gamma \sum_{s' \in S} P^{a}{ss'} v(s')$$
$$q_(s,a)=R^a_s+\gamma \sum_{s'\in S} P^{a}{ss'} \max_a' q(s',a')$$
Bellman Optimality Equation은 non-linear하므로 closed form solution이 존재하지 않고 value iteration, policy iteration, Q-learning, SARSA 등 iterative solution 이 존재한다.

MDP의 확장도 몇몇 소개하나, 그 내용이 깊게 나오지 않아 생략한다.

• Infinite and conitnuous MDPs
• Partially observable MDPs
• Undiscounted, average reward MDPs

Lecture 3: Planning by DP

DP는 optimal substructure, overlapping subproblem을 가진 경우에 대해 일반적인 해법이다. 다시 말해 하나의 큰 문제가 작은 문제들로 나뉘고 이것들이 여러 번 반복되어 다시 쓸 수 있다는 뜻이다.

MDP에서 Bellman equation이 recursive decomposition을, Value function이 해에 대해 store+reuse를 하므로 DP를 적용하기 적합하다. 이번 Lecture에서는 MDP를 DP로 푸는 방법을 소개한다.

2가지 방법, Policy Iteration과 Value Iteration을 소개한다. 둘이 사용하는 수식은 거의 비슷하지만 약간 다른데,
$$v^{k+1}=\mathcal{R}^\pi +\gamma \mathcal{P}^\pi v^k$$
$$v^{k+1}= \max_{a \in \mathcal A} (\mathcal R^a+\gamma \mathcal P^a v^k)$$
위, 아래로 각각 policy iteration과 value iteration이다. policy iteration은 policy를 두고 이를 업데이트해나가고, value iteration은 policy 없이 value function 만을 optimal value function이 되도록 수정해 나간다는 차이점이 있다.

policy iteration의 각 iteration은 크게 두 단계로 나눌 수 있다.
i) policy evaluation: 새로운 policy $\pi$에 대한 $v_\pi$를 계산한다.
ii) policy improvement: $v_\pi$에 기반해 $\pi' \le \pi$인 $\pi'$를 만들어 새로운 policy로 삼는다. 강의에서는 greedy($v_\pi$)가 $\pi'$가 되도록 한다. $\pi'(s)=argmax_{a \in A} q_\pi(s,a)$

value iteration은 별 거 없이 그냥 위 수식을 iterative하게 적용시키면 된다.

$f(v)=\mathcal{R}^\pi +\gamma \mathcal{P}^\pi v^k$는 contraction mapping이므로(참고: 3강 강의노트의 가장 마지막 부분) iteration을 반복하면 바나흐 고정점 정리에 의해 어떤 한 점으로 $v$가 수렴하며 이것이 Bellman Equation을 만족하는 최적의 가치함수가 된다.
[Iterative Policy Evaluation의 수렴성 증명]({{< ref "Iterative Policy Evaluation의 수렴성 증명" >}}) 참고.

근데 들으면서 의문이었던 게, policy iteration에서 policy improvement를 greedy하게 하면 value iteration이랑 완벽하게 똑같이 작동하는데 왜 굳이 분리하지? 싶었다. 뭐 적어도 명시적으로는 다른 꼴인데다 policy improvement를 다르게 하면 달라지니 그런가..

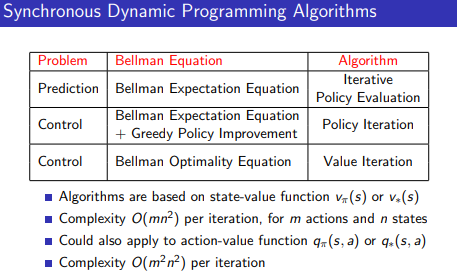
value-state function based algorithm은 $O(mn^2)$, action-value funtion based algorithm은 $O(m^2n^2)$가 소요된다.

Async DP

지금까지 소개했던 DP는 Synchronous DP, 즉 모든 state에 대한 업데이트가 병렬적으로 이루어지는 DP이다. 이에 반해 Assynchronous DP는 state의 백업을 각각, 임의의 순서로 진행한다.

이 방법을 통해 연산량을 비약적으로 줄일 수 있고 만약 모든 상태가 반복적으로 선택된다면 수렴한다고 보장되어 있다.

In-Place DP

value array의 copy를 생성해 swap하는 게 아니라, 하나의 value array에 state를 계속 업데이트하는 방식이다.

Prioritised Sweeping

$v^{k+1}(s)$와 $v^{k}(s)$의 차이가 가장 큰 $s$부터 업데이트한다. "Backup the state with the largest remaining Bellman error"

Real-Time DP

agent가 방문하는 state들부터 업데이트한다. TD와 굉장히 그 아이디어가 유사하지만, TD는 환경을 몰라도 적용 가능하다는 차이점이 있다.

(TD는 $\mathcal{R, P}$ 등을 몰라도 적용 가능하다.)

Full-Width Backups

DP는 현재 state를 처리할 때, 모든 다음 state를 고려하는 full-width backup을 사용한다. 따라서 DP는 medium-sized problems($10^6$ scale)에 적합하고, 그 이상이라면 적용이 힘들다. (강의노트에서는 curse of dimensionality를 언급하는데 무슨 맥락인지 갈피를 잡기 힘들다. 차원의 저주가 뭔지는 알지만 왜 굳이 이 맥락에..? 차원의 저주..라는 단어도 이 맥락에서 틀린 건 아니지만 그냥 '상태 수가 많은 문제'라고 간단히 서술하고 넘어가는 게 훨씬 적합하지 않나?)

Sutton의 저서에서도(단단한 강화학습 107p) 차원의 저주는 문제 자체에 내재한 어려움이지 DP의 문제가 아니라고 말한다.

간단히 말해, 큰 문제에서는 $s$에 대한 $next(s)$의 크기만 해도 너무 커서 처리할 수가 없다는 말이다. 이를 해결하기 위해 Sample Backups의 개념을 소개하는데,

Sample Backups

모든 다음 state가 아니라 일부 다음 state만을 sampling해 사용한다...는 말인 줄 알았는데
강의노트 맥락을 보니 그냥 "agent가 방문하는 다음 state", 다시 말해 단일한 다음 state만을 사용한다는 말인 듯하다. 이거 그냥 SARSA 등등 model-free RL agent를 모두 가리키는 말 아닌가..?
뭐 예를 들어 effective한 일부 다음 state만을 sampling한다든지 그런 개념을 기대했는데, advantage에 model-free 같은 게 적혀 있는 걸 보아 아닌 듯하다. 뭐 한 슬라이드만으로 완전히 설명한 건 아니겠지만.

Approximate DP

$v(s)$ 대신 approximator $\hat{v}(s)$를 사용한다. parameter $w$ 같은 것도 같이 인자로 넣어 $\hat{v}(s, w)$로 표기하기도 하는 듯하다.
대충 설명 보니 내가 sample backups에서 기대했던 거랑 비슷한 걸 하는듯. $\tilde{S} \subseteq \mathcal{S}$ 를 추출해서 이 state들에 대해 approximator을 이용해 $\tilde v_k(s)$를 계산한다.

Banach Fixed-Point Theorem

이후 36p부터 뭐 잡다한 내용 소개하는데, 간단히 말해 바나흐 고정점 정리(강의노트에서는 Contraction Mapping Theorem으로 언급)에 의해 iteration methods가 수렴한다는 이야기다.

Lecture 4: Model-Free Prediction

이번 강의에서는 model-free, 즉 모델 없이 unknown MDP의 value function을 predict 내지 estimate하는 법을 배운다. (다음 강의에서는 이 value function을 최적화하는 방법을 배운다.)

Monte-Carlo(MC)

$$v_\pi(s)= E_\pi(G_t | S_t=s)=E_\pi(R_{t+1}+\gamma R_{t+2}+\ldots | S_t=s)$$
agent가 $\pi$에 따라 episode들을 진행하도록 만든 후 그 결과에 따라 $v_\pi(s)$를 평가한다. 업데이트는 오직 하나의 episode가 끝날 때마다 된다.

알고리즘은 episode 도중 $N(s) \leftarrow N(s)+1, S(s) \leftarrow S(s)+G_t$ 후에 episode가 끝난 후에 $V(s)=S(s)/N(s)$가 되도록 짜면 된다.

크게 first-visit MC와 every-visit MC로 나뉜다. 전자는 하나의 episode에서 어떤 state를 처음 방문했을 때만 $N(s), S(s)$를 변경하고 후자는 방문할 때마다 변경해주는 것이다.

두 방식 모두 모든 state를 충분히 방문한다는 가정 하에 대수의 법칙에 의해 결과가 같지만, 그렇지 않을 경우 variance&bias에 차이가 존재하게 된다. 아마 기억 상 first-visit MC가 unbiased, high variance일거고 every-visit MC가 biased, low variance으로 알고 있다. (확인 필요함) 일단 연구가 오래 전부터 이루어진 쪽은 first-visit이라면서 first-visit 중심으로 Sutton의 책에서는 설명한다.

Blackjack Example에서 카드 합이 20 이상이면 stick하고 아니면 twist하는 무슨 근거인지 모르겠는 policy를 쓰는데, 왜 이걸 쓰냐면 아직 4강에서는 policy optimise를 어떻게 하는지 안 배웠기 때문이다 ^^;

아무튼, MC는 incremental하게 업데이트할수도 있다. $N(s):=N(s)+1, V(s):=V(s)+\dfrac{1}{N(s)}(G-V(s))$. 이 떄 $\dfrac{1}{N(s)}$를 $\alpha$로 설정하면 예전 데이터를 효과적으로 잊어버리게 할 수 있다.

$$V(s):=V(s)+\alpha (G-V(s))$$

Monte-Carlo 방법의 다양한 측면에 대해서는 Sutton의 저서에서 매우 잘 설명하고 있으며, 특히 5장 10절의 요약은 꼭 읽어 보기를 권한다. 그 내용을 여기에 쓰기보다 그냥 직접 읽는 게 나을 거라 판단했다.

Temporal-Difference Learning(TD)

현재 시점 $t$에서 상태 $S_t$의 가치 $V(S_t)$를 바로 다음 시점 $t+1$에 수정하는 방식이다. 이 때 Markov property를 이용해 return $G_t$를 $R_{t+1}+\gamma V(S_{t+1})$로 추정한다.
$$V(S_t):= V(S_t)+\alpha(R_{t+1}+\gamma V(S_{t+1})-V(S_t))$$
$\delta_t:=R_{t+1}+\gamma V(S_{t+1})-V(S_t)$는 TD error이라 불리고, $R_{t+1}+\gamma V(S_{t+1})$은 TD target이라 불린다.

Bias-Variance Trade-Off

return $G_t$가 unbiased estimate of $v_\pi(S_t)$인에 반해, TD target은 같은 통계량의 biased estimate이다. 하지만 TD는 겨우 한 스텝의 action, transition, reward에 의존하므로 훨씬 낮은 variance를 가진다. (Bias-Variance Tradeoff)

MC vs TD vs DP 시각화

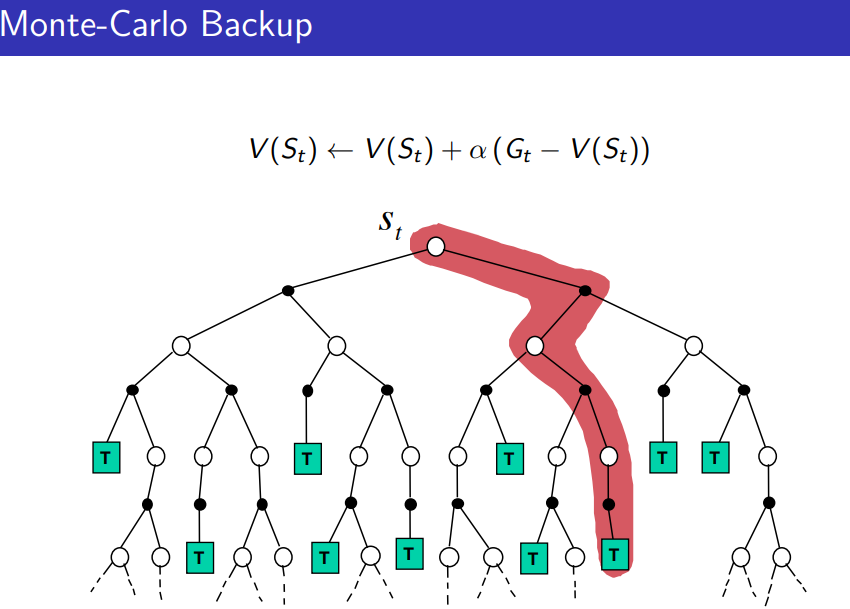
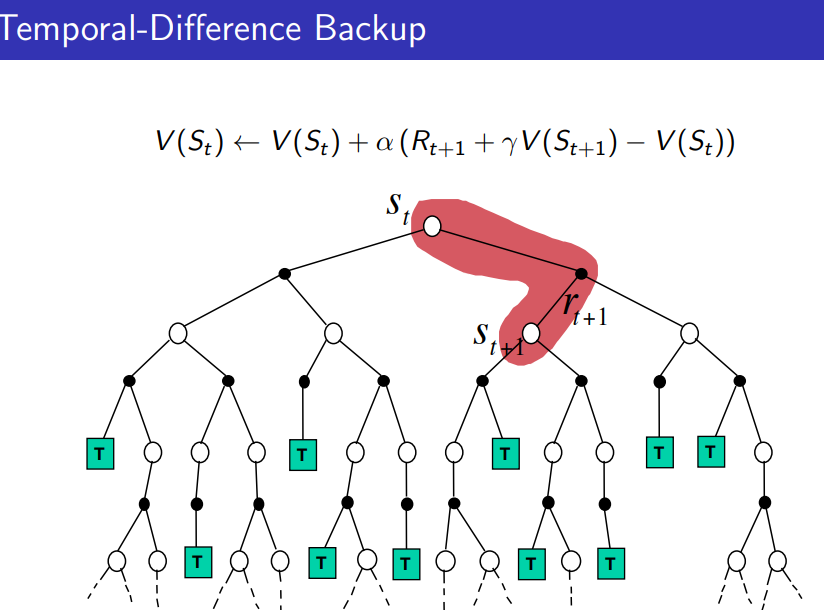
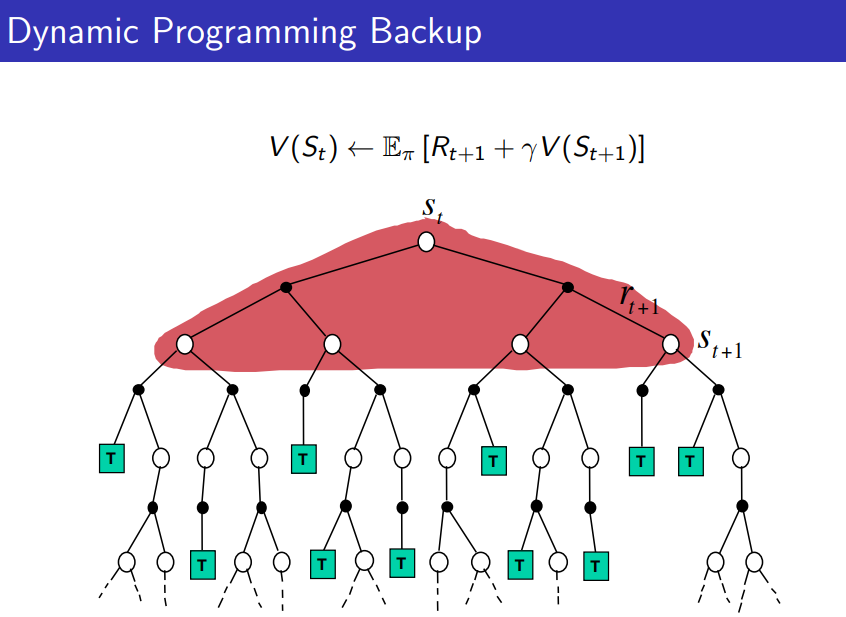
Bootstrapping and Sampling

Bootstrapping: 업데이트가 추정을 포함(MC X, DP O, TD O)
Sampling: 업데이트가 샘플을 이용(MC O, DP X, TD O)

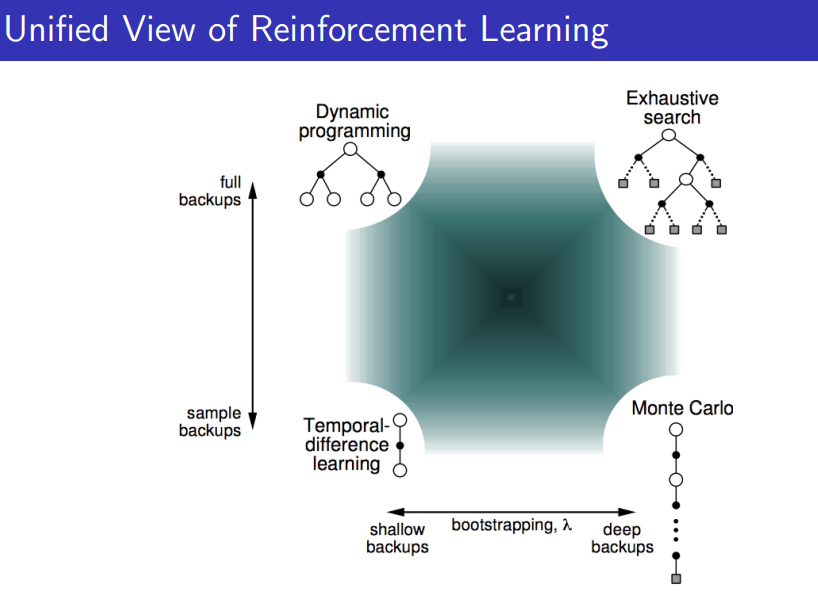
TD($\lambda$)

TD가 미래의 $n$개 step을 본다고 하자. 미래의 1개 step만 본다면 TD고, $\infty$개 step을 본다면 MC와 같다.
이러한 $n$은 크지도 작지도 않게 잘 맞춰야 학습 성능이 잘 나온다.

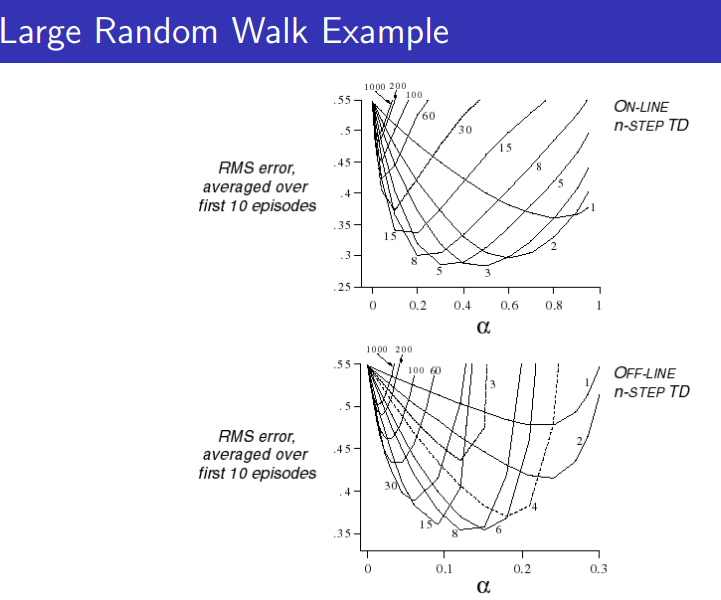
$n$개의 미래를 봤을 때 return 추정량을 $G^{(n)}$으로 표기하자. 그럼 예를 들어, 2-step과 4-step의 return 추정량의 반인 $\dfrac{1}{2}(G^{(2)}+G^{(4)})$을 사용하면 성능이 더 좋아지지 않을까?

이러한 아이디어에서 $\lambda$-return을 이끌어낼 수 있다. 미래 시점으로 갈수록 반영도가 $\lambda$에 따라 감쇠되며 가중치 총합이 1이 되도록 설계한 것이다.
$$G_t^\lambda=(1-\lambda)\sum_{n=1}^\infty \lambda^{n-1}G_t^{(n)}$$
$\lambda$ 역시 적당한 중간 값을 찾아야 좋은 성능이 나온다.

크게 Forward-view와 Backward-view TD($\lambda$)로 나눌 수 있다.
Forward-view TD($\lambda$): $V(S_t):=V(S_t)+\alpha(G_t^\lambda -V(S_t))$
Backward-view TD($\lambda$): $V(s):=V(s)+\alpha \delta_t E_t(s)$

이 때 $E_t(s)= \gamma \lambda E_{t-1}(s)+\mathbb{1}(S_t=s)$, $\delta_t$는 TD error
$E_t(s)$는 state $s$가 현재 시점까지 $t_1, t_2, t_3, \ldots$에 나왔으면 $E_t(s)=\sum (\gamma \lambda)^{t-t_i}$꼴이 되고 미래의 TD error에 $(\gamma \lambda)^{시간차이}$가 곱해져 더해지는 꼴이기에 결국 forward-view와 똑같은 결과를 낸다는 것을 알 수 있다.

TD(0)는 1개의 state만 업데이트되는 TD랑 똑같고 TD(1)는 MC(every-visit)랑 똑같다...고는 하는데 수식 상 Forward-view TD는 그렇지 않고 Backward-view TD만 그런 것 같다. 아마 $\lambda$에 따른 수렴반경과 관련있는 듯한데($\lambda=1$이면 가중치 합이 1이 될 수 없음) 뭐 어차피 $\lambda=1$로 둘 경우 그러느니 차라리 MC를 쓸테니 크게 중요한 부분은 아닌듯.

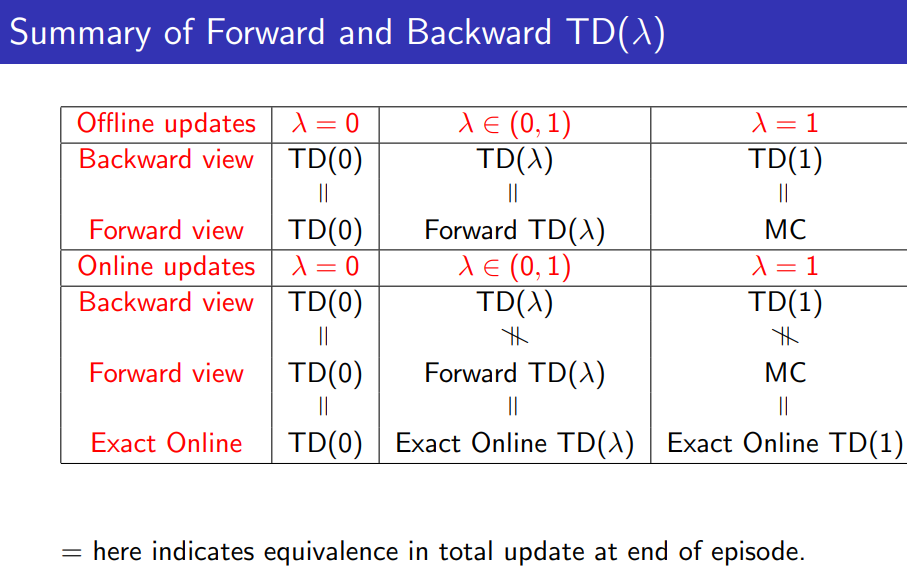
online vs offline

value function을 episode 시행 도중 업데이트하면 online, episode가 모두 끝나고 시행하면 offline이다. 그 예시로 TD(1)을 offline으로 사용하면 MC(every-visit)과 똑같다.

Online updates에서 Forward-view와 Backward-view TD($\lambda$)는 조금의 차이점을 보이나 새로운 연구에서 같게 할 수 있도록 수식을 수정했다고 David Silver의 강의노트에는 나온다. 근데 애초에 같도록 수식을 짜는 게 더 자연스럽지 않나.. 라는 생각도 들고 아마 2015년 강의에서 "새롭다"라고 했으니 지금은 새롭지 않을 듯하다. (ICML 2014, Sutton and von Seijen)

Lecture 5: Model-Free Control

드디어 Model-Free RL Agent에 대해 policy를 최적화하는 방법을 배운다.

Model-Free Control을 사용하는 경우

1. MDP model이 알려져 있지 않으나(환경을 모름) 경험은 샘플링 가능할 때
2. MDP model이 알려져 있으나 너무 커서 샘플만 사용할 수밖에 없을 때

On-policy vs Off-policy

Agent가 환경과 상호작용하는 policy와 업데이트하고 싶은 policy가 다를 수 있다. 이렇게 $\mu(\mu \ne \pi)$(행동 정책, behaviour policy)에서 샘플링된 경험에서 $\pi$(목표 정책, target policy)를 업데이트하면 Off-policy라고 부르며, $\pi$에서 샘플링된 경험에서 $\pi$를 업데이트하면 On-policy라고 부른다.

Behaviour Policy가 달라야 유용한 이우: Exploration이 필요하기 때문
단, Exploration이 많아질수록 수렴이 느려진다. (Exploration-Exploitation dilemma)

Off-policy agent는 on-policy agent에 비해, 데이터가 서로 다른 정책에서 비롯되기에 분산이 크고 수렴 속도가 느리다. 하지만 더 일반적이며 강력하다.

$\epsilon$-greedy란: $\epsilon$(보통 적당히 작은 수)의 확률로 exploration, $1-\epsilon$의 확률로 greedy choice(보상을 최대화하도록)을 하도록 한다.

Greedy in the Limit with Infinite Exploration(GLIE)

$\epsilon$-greedy가 수렴하기 위해서는 모든 state-action pair가 무한번 방문되어야 하며 policy가 greedy policy에 수렴($\epsilon \rightarrow 0$)해야 한다.

예를 들어 episode 시행 횟수 $k$에 따라 $\epsilon=\dfrac{1}{k}$로 만들면 될 것이다.

SARSA

state S에서 action A를 해 reward R을 받고 state S'에 가 action A'를 한다. 그리고 그 즉시 value function을 업데이트
$$Q(S,A):=Q(S,a)+\alpha(R+\gamma Q(S',A')-Q(S,A))$$
갑자기 왜 SARSA 이야기를 하냐면, David Silver의 강의노트에서는 먼저 $\epsilon$-greedy MC 설명을 하고 "에피소드가 끝났을 때만 업데이트하는 게 아니라 online하게 업데이트할수도 있다!" 고 알려주려고 하는 듯하다.

SARSA: online, on-policy RL agent

SARSA는 GLIE와 Robbins-Monro sequence of step-sizes $\alpha_t$를 만족할 때 optimal action-value function에 수렴한다.

• Robbins-Monro sequence of step sizes $\alpha_t$
  $\sum_{t=1}^\infty \alpha_t = \infty, \sum_{t=1}^\infty \alpha_t^2 < \infty$
  뜻: $Q(s,a)$를 무한한 곳까지 데려갈 수 있지만 step size가 점점 작아져 수렴해야 한다.
  근데 도대체 왜 세제곱도 네제곱도 아니고 제곱이 유한하다고 했는지는 꽤 궁금한데 간단히 찾아봤을 때는 안 나왔다. 아마도 $\sum \alpha_t^2$에 비례해 수렴 시간이 정해지는 게 아닐까 싶은데..

당연히 $G_t$ 뿐만 아니라 $G_t^\lambda$도 사용 가능하다.
forward-view, backward-view SARSA($\lambda$) 소개하는데 생략

Off-policy

Behaviour policy $\mu$와 Target policy $\pi$가 다를 때
조건부확률에 기초해 $G_t^\mu$ 대신 $G_t^\pi$를 구해 $V_\mu(S_t)$ 대신 $V_\pi(S,t)$에 가치 함수가 수렴하도록 만들어야 한다.

David Silver의 강의에서는 단순히 조건부확률에 기초해 $\alpha(G_t^{\pi/\mu}-V(S_t))$만큼 $V(S_t)$를 업데이트하고, Sutton의 저서에서는 중요도추출법(importance sampling)을 이용해 기본 중요도추출법(orginary importance smapling)과 가중치 중요도추출법(weighted importance sampling)을 설명한다.

기본 중요도추출법은 target policy와 behaviour policy에 따라 unbiased, high variance(심지어 분산이 무한대가 될 수도 있다)이고 가중치 중요도추출법은 low variance인데 적은 양의 표본에서 biased이다. (물론 충분히 많이sampling이 되면 unbiased하게 수렴한다.) 자세한 내용은 Sutton의 저서를 참고하라.

Sutton의 저서가 더 formal하게 잘 설명되어 있는 듯하지만 짐작하기로 David Silver의 강의대로 그냥 $\alpha$랑 오차 곱해서 업데이트해도 실전적으로는 문제 없을 것 같아서 강의에서 그렇게 소개하는 것 같다.

Off-policy online learning: Q-Learning
$$Q(S_t, A_t):=Q(S_t, A_t) + \alpha (R_{t+1}+\gamma Q(S_{t+1}, A')- Q(S_t, A_t))$$
$A_{t+1}\sim \mu(\cdot|S_t)$ 대신 $A'\sim \pi(\cdot|S_t)$ 를 이용해 $Q(S_t, A_t)$를 업데이트한다!

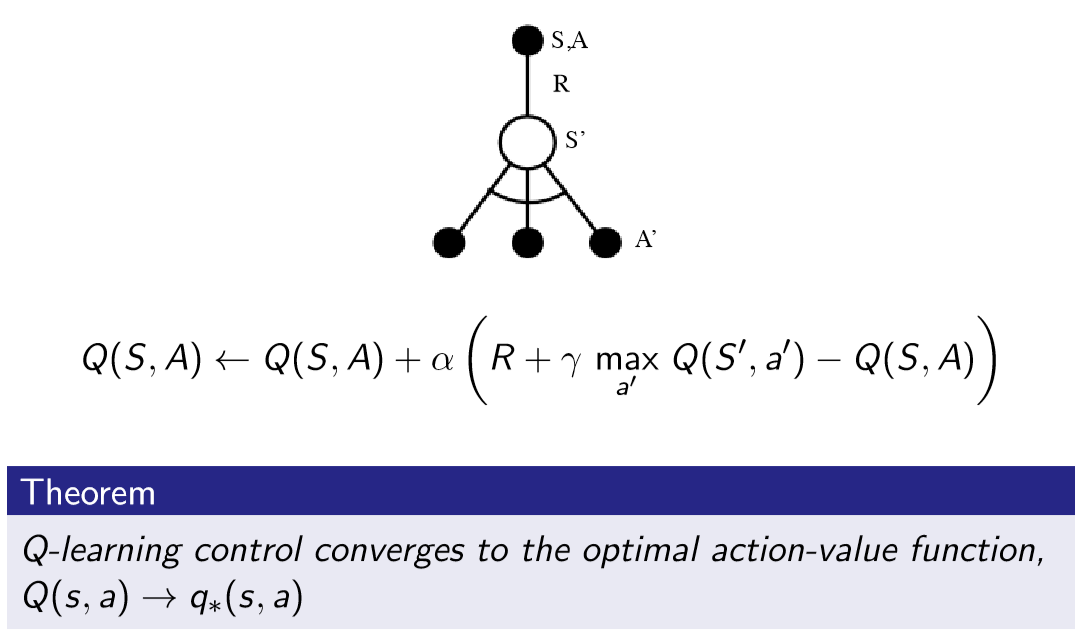
$Q$에 greedy하게 $\pi$를 골랐을 때, SARSA와 대비해 모든 action 중 최대의 $Q$를 얻는 action을 선택하므로, SARSA와 대비해 보강 다이어그램에 $S'$ 아래에 여러 개의 $A'$를 그려넣을 수 있다. SARSAAA? 그래서 Q-learning은 SARSA Max라고도 불린다고 한다.

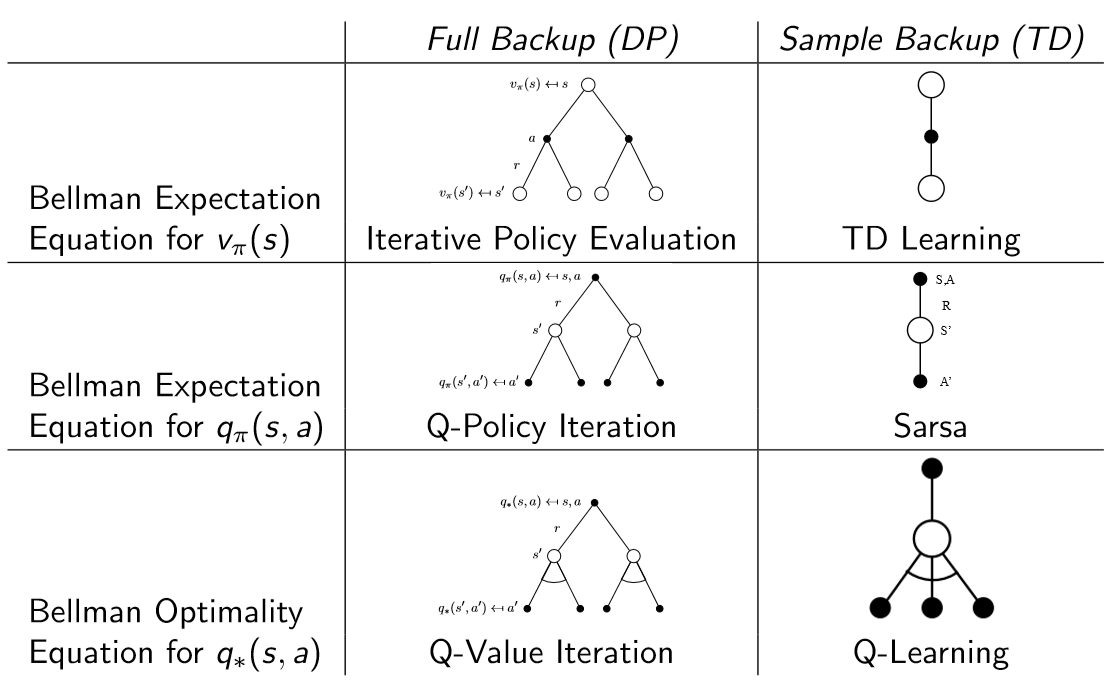
Lecture 6: Value Function Approximation

이번 Lecture에서는 value function을 근사하는 방법을 배운다. function approximation을 위해 parameter $w$를 도입한다.
$$\hat{v}(s, w)\sim v_\pi(s)$$
우리의 목표는 가장 잘 $v_\pi$를 근사하게 만드는 parameter $w$를 찾는 것이다.

large MDP의 문제: 너무 많은 state and/or action이 존재하여 lookup table 기반의 value function 구성이 불가능하다. 따라서 value function을 근사한다.

기본 개념은 supervised 머신러닝과 같다. seen data(seen state)를 generalise하여 unseen data(unseen state)에 대한 함숫값을 추론하는 것이다.

Stochastic Gradient Descent 등 여러 기법을 이용하기 위해 function approximator은 differentiable해야 유리하다. 그러한 function approximator의 예시로는 선형 모델과 Neural Network가 있다.

다만 supervied-learning의 많은 경우 다루는 "데이터의 iid 분포" 전제와 다르게, Reinforcement Learning 문제에서는 데이터(state)간의 연관성이 커 non-iid라고 봐야 하는 경우가 많고 non-stationary한 경우도 많다. 또한 supervised learning과 다르게 supervisor이 없고 reward만이 존재하기에 즉각적인 피드백이 어렵다.

error funtion을 다음과 같이 정의하고 $\Delta w = -\dfrac{1}{2}\alpha \nabla_w J(w)$와 같이 gradient descent를 돌릴 수 있다. gradient descent와 학습 전반에 관련된 설명은 RL 강의가 아니어도 많은 곳에서 설명하기에 생략한다.
$$J(w)=E_\pi\left[\left(v_\pi(S)-\hat{v}(S, w)\right)^2\right]$$
물론 전체 $S$가 아닌 sampling된 일부 state $\tilde{S} \subseteq S$에 대해 gradient descent를 실행하면 Stochastic gradient descent가 된다.

linear function approximator

$x(S)=\begin{bmatrix}x_1(S)\\vdots\x_n(S)\end{bmatrix}$를 feature vector라고 하자. 이는 state $S$를 입력으로 받아 이것의 표현형 $x(S)$를 반환해주는 함수이다.

$\hat{v}(S, w) =\langle x(S), w \rangle= x(S)^T \cdot w$로 두면 이는 value function을 $x_i(S)$의 linear combination으로 나타내는 것이다. 특히 이 때 loss function은
$$J(w)=E_\pi\left[(v_\pi(S)-x(S)^Tw)^2\right]$$
그리고 $\Delta w =-\dfrac{1}{2} 2 \alpha (v_\pi(S) - x(S)^T w) (-x(S))=\alpha (v_\pi(S) - \hat{v}(S, w)) \cdot x(S)$가 된다. 특히, $x_i(S)=\mathcal{1}(S=s_i), w_i=V(s_i)$일 때, table lookup value function과 $\hat{v}(S, w) = \mathcal{1}^T \cdot w$는 완벽하게 같은 역할을 하고 $\Delta w$도 이전에 논의했던 것과 완전히 똑같다. 다시 말해, function approximation을 하는 경우는 function approximation을 하지 않은 경우를 포함하며 이는 자연스러운 결론이다.

$$\hat{v}(S, w)=\begin{bmatrix}\mathbb{1}(S=s_1)\\mathbb{1}(S=s_2)\\vdots\\mathbb{1}(S=s_n)\end{bmatrix}^T \cdot \begin{bmatrix}w_1\w_2\\vdots\ w_n\end{bmatrix}$$

MC, TD(0), TD($\lambda$)

물론 RL에는 true value function $v_\pi(S)$가 없다. 따라서 MC의 return $G_t$, TD($\lambda$)의 return $G_t^\lambda$ 등을 $v_\pi(s)$에 대신 넣어줘야 한다.

요약하면 $\langle S_t, G_t \rangle$를 supervised learning의 training data처럼 써줘도 된다.

MC evaluation을 했을 때, $G_t$는 가치함수의 unbiased+noisy 추정값이 된다. parameter은 local optimum으로 수렴하고, function approximator으로 non-linear function을 사용해도 variance가 클 수 있지만 수렴하게 된다.

TD-target은 biased sample of true value $v_\pi(S_t)$이고, linear TD(0)는 global optimum에 '가깝게' 수렴한다. TD($\lambda$)도 biased sample이고 수렴성 관련해서는 강의노트에 뭐가 없는데 뭐가 어디에 있겠지?

mountain car example

Linear SARSA mountain car example을 보여주는데, $x,v,a$의 관계에 대한 지식 없이 학습시키다보니 어려운 듯하다.

정리

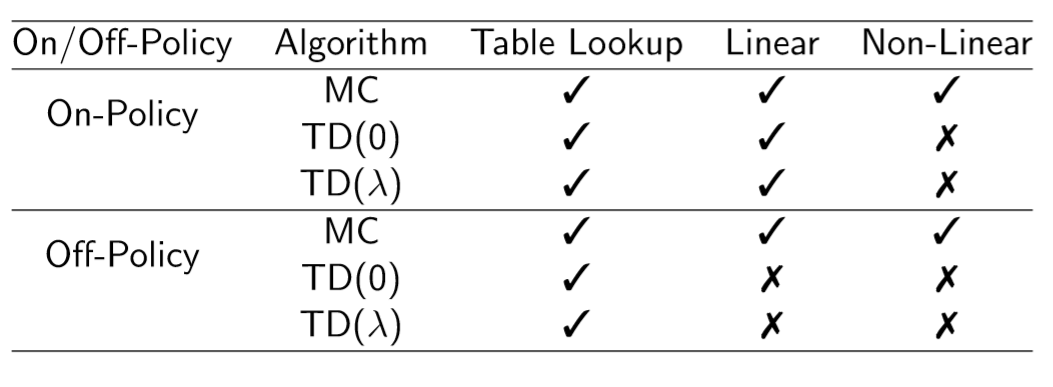
on->off policy, MC->TD($\lambda$)로 갈수록 수렴성이 좋지 않으며, 수렴성이 설령 보장되어있지 않더라도 실제 환경에서 잘 작동하는 경우도 많다.

linear TD가 수렴하지 않는 반례를 보여주는데 Baird's counter-example이라고 꽤 유명한 반례인 듯하다. (parameter가 발산한다)

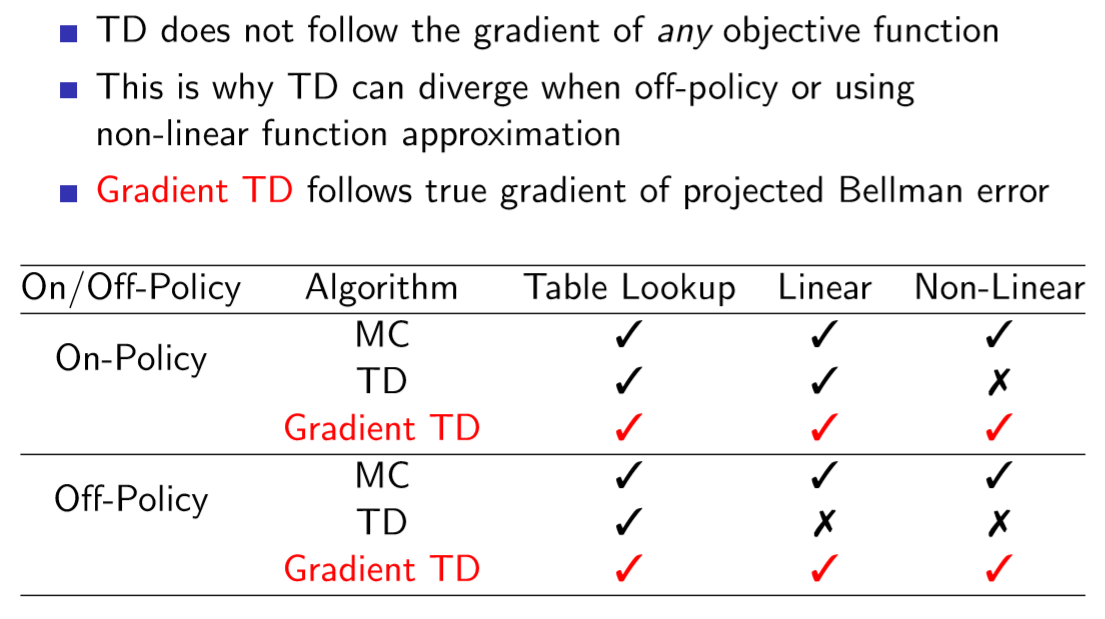
그 와중에 TD인데 수렴하는 TD라고 Gradient TD를 보여준다. Sutton의 저서에는 자세히 나와 있으나 강의에는 없는듯..

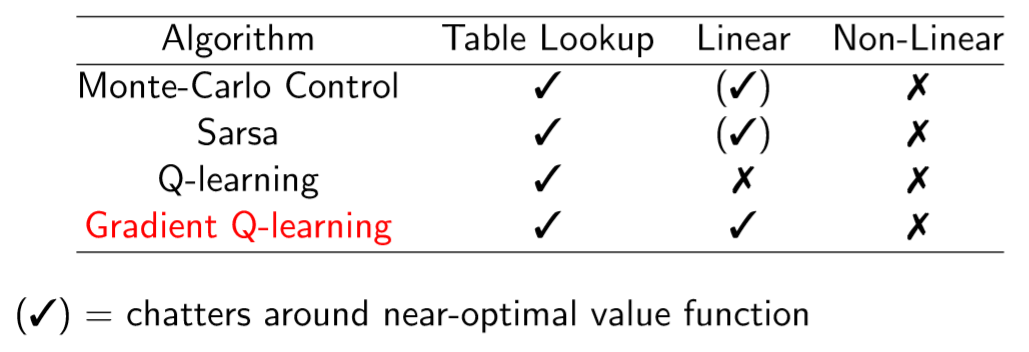
control 문제에서도 Gradient Q-learning은 이론상 수렴한다.

DQN(★)

필요하다면 https://engineering-ladder.tistory.com/68 을 참고하라.

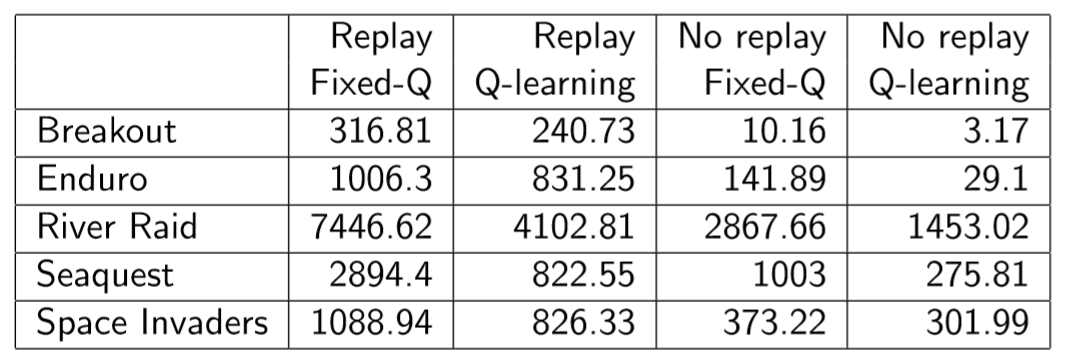
NN based Q-learning을 RL에 적용할 때, 인접한 경험 사이 연관성이 지나치게 높다는 점을 해결하기 위해 experience replay를 도입한다. (인접) 데이터의 iid 분포가 깨지면 SGD의 수렴성이 보장되지 않는다.

• Experience Replay(NIPS, 2013)
  replay memory buffer $\mathcal{D}$는 FIFO 형식의 자료구조로, 기억하기로 일정 용량이 정해져 있어 그 이상 데이터가 추가되면 데이터를 삭제했던 것으로 기억한다. state $s_t$를 전처리한 $\phi_t$에 대해 $(\phi_t, a_t, r_t, \phi_{t+1})$을 $\mathcal{D}$에 계속 삽입하며 이 중 랜덤한 미니배치를 뽑아내 매 시간 학습을 진행하는 것이 experience replay이다. Experience replay를 통해 학습 데이터의 독립성을 어느 정도 확보할 수 있다.

• Fixed Q-Targets(Nature, 2015)
  $v_\pi(s)$의 추정값(target value) $y_j$를 일정 시간(step $C$) 동안 고정시킴으로써 성능을 향상시켰다. 타겟과 그 근방이 계속 이동하는 것을 막아 학습이 안정적으로 이루어지게 한다. lookup table과 대비해 NN-based policy는 단일한 state가 아닌 state의 근방을 업데이트하므로 autoregressive한 업데이트가 계속 이루어져 학습이 불안정하게 이루어지게 만들어서 그런 듯한데(내 추측이다), 자세한 이유는 설명하는 곳이 없어 아쉽다. 내 추측이 맞는지도 궁금하고.

Lecture 7: Policy Gradient

Lecture 6에서는 $V^\pi(s)$의 approximator $V_\theta(s)$, $Q^\pi(s,a)$의 approximator $Q_\theta(s,a)$를 소개했다. 이 때 policy는 value function에서 직접적으로 파생되었으며(예를 들어 $\epsilon$-greedy) 이번 Lecture에서는 policy를 model-free하게 parametrise하는법을 소개한다.

Value Based->Learnt Value Function, Implicit Policy(e.g. $\epsilon$-greedy)
Policy Based->Learnt Policy Function, No value function
Actor-Critic->Learnt Value Function + Leanrt Policy

Policy-based RL의 장점

• 더 좋은 수렴 성질을 가진다.
• 고차원 혹은 연속적인 action space에 효과적이다.
• 확률적 policy를 배울 수 있다. ($\epsilon$-greedy는 'greedy'이기에 $\epsilon$이 아니면 policy가 정해져 있다.)
  단점
• glocal optimum보다 local optimum에 수렴
• policy evaluation은 보통 비효율적이며 high-variance

Value Based는 max만을 취하기에 aggressive한 방법론이고 Policy Based는 parameter을 gradient에 따라 미세하게 업데이트하기에 stable한 방법론이다.

Policy-based가 필요한 예시를 제시한다. 만약 어떤 칸에서 인접한 한 칸만 관측이 가능하다면(partially observable) 아래의 회색 칸은 구분이 불가능하고, $\epsilon$-greedy나 greedy policy를 사용하면 두 회색 칸에서 모두 왼쪽으로 가거나 오른쪽으로 가야 한다. 하지만 그러면 회색 칸에서 이동하는 하얀 칸에서, 해골보다 기대 가치가 높은 회색 칸으로 이동하게 될 거고, 그럼 무한 루프가 발생한다. 즉, 이 예시에서 deterministic policy가 아닌 stochastic policy가 필요하며 policy-based RL이 해법이 된다.

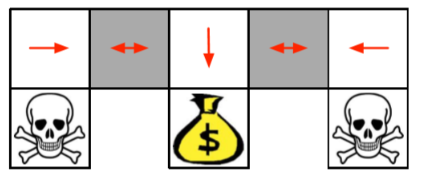
3장(DP)에서 언제나 optimal deterministic policy가 존재하며 구하는 방법을 배웠었는데, 지금 이게 성립하지 않는 것은 "Markov+Fully observable"에서 "Fully observable"이 빠졌기 때문이다.

Policy Objective functions

Policy가 얼마나 좋은지 어떻게 판단할까?

1. start value
2. averge value
3. average reward per time-step

이 때 $d^{\pi_\theta}$는 마르코프 체인의 stationary distribution(무한 시간 후 그 곳에 있을 확률)

이후 GD에 대해 열심히 설명하고

어떤 objective function을 사용하더라도 gradient는 위와 같이 나타난다고 한다. 이 때 $Q^{\pi_\theta}(s,a)$의 참값은 얻을 수 없기에 추정값을 이용해야 하고

예를 들어 MC를 사용하면 MC policy gradient라 하고 이는 AlphaGo에 사용되었다고 한다.

다만 MC policy gradient는 high-variance여서 느리다. 그래서 action-value function을 추정하는 'critic'을 제시하는데, 이것이 바로 Actor-Critic Algorithm이다. policy와 action-value function 모두가 parametrize된 것이다.

actor은 방금 제시했던 대로 $\nabla_\theta J(\theta)$로 학습할 수 있다. 그렇다면, critic의 $w$는 어떻게 학습하는가? -> 바로 이전 강의에서 배웠던 것처럼, TD($\lambda$) 사용($\lambda \in [0,1]$)

여기다 baseline을 state-value function으로 삼아 빼주면 분산을 상당히 낮출 수 있다. 물론 이렇게 하려면, critic이 advantage = Q-V를 구해야 하므로, value function 역시 추정해야 한다.

TD Error을 잘 추정하면 advantage function을 구할 수 있다.

policy gradient의 여러 형태

Lecture 8: Integrating Learning and Planning

이전의 강의에서는 경험에서 policy와 value function을 배우는(Actor-Critic) 것을 배웠다. 이전 강의에서 배운 RL Agents는 모두 model-free로, 모델이 없다. 이번 강의에서 배울 것은 model을 경험에서 배우고 planning을 이용하는 RL agent이다.

• Model-Based RL: Learn a model from experience + Plan value function(and/or policy) from model

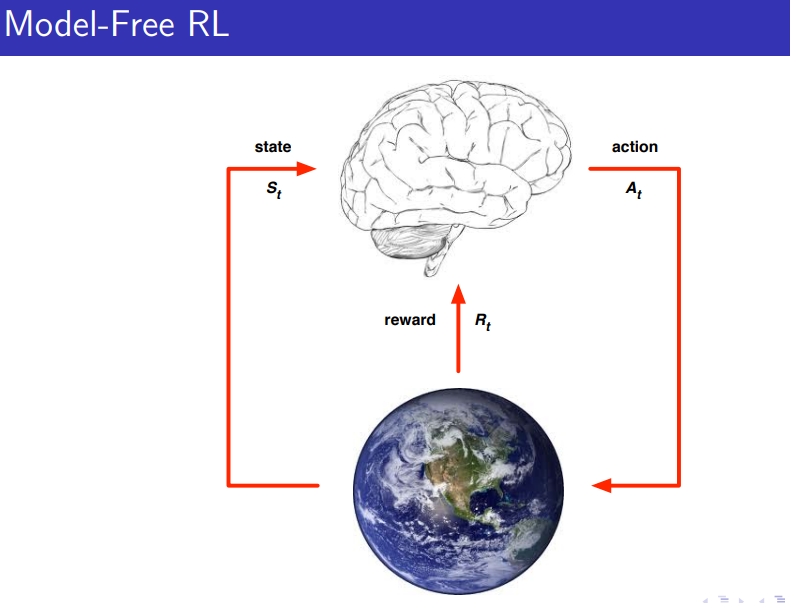
Model-Free vs Model-Based를 재치 있게 나타낸 그림이다.
일종의 가짜? 가상?의 지구를 만든다고 생각하는 것이다.

Model

model $\mathcal{M}$은 MDP $\langle \mathcal{S, A, P, R} \rangle$의 parameter $\eta$에 의한 근사이다.
$\mathcal{S, A}$는 알고 있다고 가정하면, $\mathcal{M= \langle P_\eta, R_\eta \rangle}$은 state transition과 reward를 $\eta$로 근사하는 것이다. 그리고 보통 어떤 시점의 reward와 다음 state는 독립적이라고 가정한다.

우리의 목표는 model $\mathcal{M_\eta}$를 성공적으로 근사하는 것이다. 이는 앞서 했던 것과 같은 supervised learning problem으로 볼 수 있다. 지금의 state와 action에 대해 reward와 다음 state를 예측하는 것이기 때문이다. reward를 예측하는 것은 regression problem, 다음 state를 예측하는 것은 density estimation problem이다. regression은 mean-square error, density estimation은 KL divergence loss function으로 사용할 수 있겠다.

Model의 종류

• Table Lookup Model
• Linear Expectation Model
• Linear Gaussian Model
• Guassian Process Model
• Deep Belief Network Model
• ...

Table Lookup Model

$\langle s,a, \cdot, \cdot \rangle$을 matching하는 기록을 찾는다.

Planning with a Model

Planning: MDP $\langle \mathcal{S, A, P_\eta, R_\eta} \rangle$을 푸는 것(optimal value function, 또는 optimal action-value function을 찾자!)

그래야 policy를 정해서 최적의 선택을 할 수 있기 때문이다.

Sample-Based Planning

추정한 $\mathcal{P_\eta, R_\eta}$에서 experience를 샘플링해 model-free RL을 적용한다.
모델을 샘플을 만드는 데에만 사용하는 것으로, 간단하지만 강력한 접근법이라고 한다.

다만 애초에 추정된 모델이 정확하지 않으면 optimal policy를 구할 수 없다는 단점이 있다. 이에 대한 해결책으로는 model-free RL을 쓰거나 모델의 불확실도를 추측하는 방법이 있다.

Integrated Architectures: Dyna

model에서 sample된 simulated experience와 environment에서 sample된 real experience를 모두 이용해 value function을 추정한다.

Forward Search

model을 이용해 앞으로 어떤 action을 선택하면 좋을지 미리 앞을 내다보는 것

Simulation-Based Search

model을 이용해 앞으로 어떻게 될 지 시뮬레이션을 돌려 가장 좋은 선택지를 구함

• Monte-Carlo Tree Search
  model을 이용해 정책 $\pi$에서 시뮬레이팅해 simulated experience를 얻어 $Q(s,a)$를 evaluate

Tree Policy(MC 결과를 이용해 구한 가장 좋을 것이라 추정되는 policy)와 Default Policy(랜덤)을 사용

• TD Search
  위와 같지만 TD 사용
  보통 MC보다 성능 좋음. TD($\lambda$)는 더 좋을 수 있음

Dyna-2

real-experience에서 얻은 long-term memory와 simualted experience에서 얻은 short-term memory 이용

value function은 long-term과 short-term 메모리의 합
이는 하나의 value function을 simulated와 real experience 모두로 업데이트하는 이전과 다르다.

Lecture 9: Exploration and Exploitation

Exploration and Exploitation Dilemma는 이쯤 되면 다 알 만 하니 넘어가고

• Regret: 간단히 말하면 얻지 못한 보상(물론 수학적으로는 좀 더 세심히 정의해야 하지만). 누적 보상을 최대화하는 건 총 regret을 최소화하는 것과 같다.

이후 UCL 등을 이용해 룰렛문제를 푸는 방법을 제시한다.

Lecture 9 내용은 이후.. 생각이 나면..? 업데이트 예정

전체 요약

Markov 기본 전제 하에서

Known MDP: DP로 풀이 가능(중간 크기 문제)

• Value Iteration(벨만 최적 방정식을 대입꼴로 반복), Policy Iteration(policy eval+policy improvement 반복)

Unknown or large MDP(model-free): TD($\lambda)$로 풀이(이는 MC, TD(0) 포함)
model-free control: on-policy는 off-policy로 일반화 가능, off-policy는 parameterized-policy로 일반화 가능

결국 policy와 value 모두 parametrize 한 것: Actor-Critic

Learning과 Planning을 합치는 것(Lecture 8): simulated experience + real experience 섞어서 이용

사실 그래서 결국은 Actor-Critic을 특수화하면 7강까지의 모든 내용이 나온다.
생각보다 내용이 크게 없다. 하지만 이러한 핵심적인 내용만으로도 '간단하지만 powerful'하고.. 거기다 강화학습은 무언가 강의에서 소개할 만한 fundamental한 내용이 이달리 뭐가 없어서 이렇게 소개해 주는듯.

강의 내용에 더해 DQN(강의에서도 소개해 주기는 하나 약간 빈약하다), A3C 정도 확실하게 공부하고 넘어가면 도움이 될 듯하다.

내가 보진 않았지만 좋아 보이는 레퍼런스: https://dnddnjs.gitbooks.io/rl/content/