미분방정식 정리 06 - Systems of Differential Equations
Systems of First-order Linear Differential Equations
\[\frac{d}{dt} \left[ \begin{matrix}x_1 \\ x_2 \end{matrix} \right] =\left[ \begin{matrix}a & b\\ c & d \end{matrix} \right] \left[ \begin{matrix}x_1 \\ x_2 \end{matrix} \right]\]
위와 같이, $\dot{x}=Ax$인데, 실수(또는 복소수) 대신 벡터와 행렬을 다루는 미분방정식에 대한 풀이법을 소개한다.
이전과 마찬가지로 $X(t)=ve^{\lambda t}$로 해를 Guess 했을 때 $\lambda v e^{\lambda t}= Ave^{\lambda t}$에서 $Av=\lambda v$이고, 따라서 $v$, $\lambda$는 각각 eigenvector와 eigenvalue가 된다. eigenvalue가 중근을 가질 때에 대한 해법은 소개하지 않으나, eigenvalue가 전부 서로 다르다면 각각의 "짐작된 해" $X(t)=ve^{\lambda t}$가 해공간의 기저 역할을 수행할 수 있으므로 이들의 선형결합 형태로 일반해가 나타난다.
\[X(t)=\sum_k c_k v_k e^{\lambda_k t}\]
고윳값이 실수든 복소수든 똑같이 위 수식 쓰면 된다.
$x,A$를 스칼라에서 벡터와 행렬로 확장시키며 중간에 기저변환행렬도 이용하는 일반해 유도 방법은 아래 링크 참고.

하나 유의할 점은, 강의 설명에서는 복소수 고윳값이 나와도 해 $X(t)$로는 실수값만 취한다는 것이다. 왜 그런지 강의에서는 설명을 안 해서 나도 이유가 궁금한데, 짐작하기로는 보통 미분방정식은 물리적 시스템을 기술하기 위해 쓰이는데, 물리량의 경우 허수 부분이 관측되지 않아(표현이 정확한지 모르겠다) 그런 것 같기는 하다.
또 유의할 점은, 아무래도 강의에서 실수 field의 미분방정식만을 다루는 것 같다. 복소수 field로 가면 두 고윳값의 실수부가 달라지는 등 문제가 생길 수 있어 보이는데 흠... 고윳값의 실수부가 서로 달라도 사실 본질적으로 큰 문제는 없지만 그걸 가정하고 phase portrait 등을 그리는 것 같다.
Practice Quiz: Systems of Differential Equations
답
3,2,4
Phase Portraits
이 부분은 시각적 묘사가 굉장히 중요한 부분으로, 이 블로그에 줄글로 설명하기엔 조금 무리가 있다. 애초에 이 글은 미분방정식 "정리" 시리즈이므로 그렇게 자세하게 설명할 생각은 없었지만 그래도 이해가 안 된다면 https://youtu.be/UO_dgXa5szg 이 영상을 참고하자.
Phase Portraits
Phase Portraits이란, 2변수 미분방정식에 대해 해 $X_1, X_2$가 시간에 따라 그리는 궤적을 나타낸 것이다. (위에서 말했듯 $X_1, X_2$이 실수값을 가지므로 2차원 좌표평면 위에 나타낼 수 있다.)
Fixed Point로 $(X_1, X_2)=(0,0)$을 잡는데, 왜 $(0,0)$을 Fixed Point로 잡는지는 조금 설명을 더 보면 알 수 있다.
- Eigenvalue 2개가 실수이며 음수: stable node
- Eigenvalue 2개가 실수이며 양수: unstable node
- Eigenvalue 2개가 실수이며 +, -: saddle point
- Eigenvalue 2개가 복소수이며 Real part가 음수: stable spiral
- Eigenvalue 2개가 복소수이며 Real part가 양수: unstable spiral
Stable and Unstable Nodes
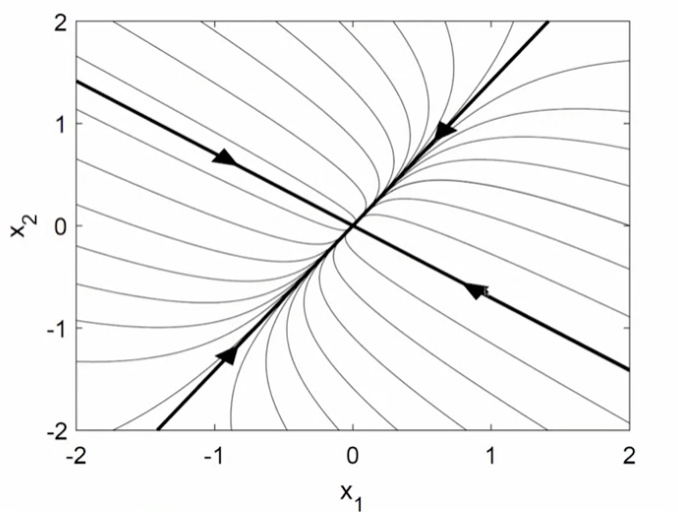
\[x=c_1 \left(\begin{matrix} 1 \\ -\frac{1}{\sqrt{2}}\end{matrix} \right) e^{-4t}+c_2 \left(\begin{matrix} 1 \\ \sqrt{2}\end{matrix} \right) e^{-t}\]
위의 일반해를 시각화한 것으로, $t$가 무한대로 갈수록 $x_1$과 $x_2$ 모두 0으로 수렴해 이동하는 것을 알 수 있다. 특히, $c_1=0$ 또는 $c_2=0$일 때를 굵은 선으로 표시한 것에 유의하자. 이 선들이 나중에는 점근선이 되기도 한다.
Saddle Points
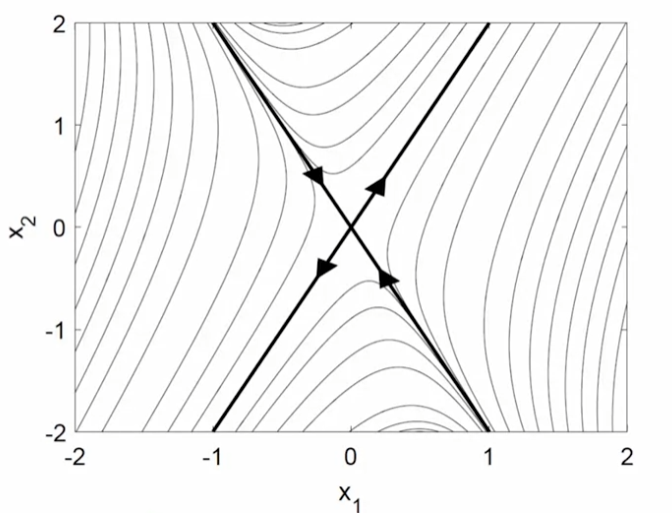
$e^{\lambda_1 t}, e^{\lambda_2 t}$중 하나는 $t \rarr \infty$에 따라 무한대로 발산하고 하나는 0으로 갈 때 위와 같이 그림을 나타낸다.
한 방향으로는 stable하고 한 방향으로는 unstable한 것이 말의 안장(saddle)과 닮았다 하여 saddle points라고 한다고 한다. 근데 point가 아닌데 왜 point라고 하지?
조금 특기할 만한 점은 수렴하는 직선 위에 있으면 fixed point에 결국 도달하게 되고, 그보다 조금이라고 벗어나 있으면 발산항에 영향을 받음을 따라 (0,0)에서 무한히 멀어진다는 점이다. 물리적으로 주목할 만한 의미가 있을지도.
Spirals
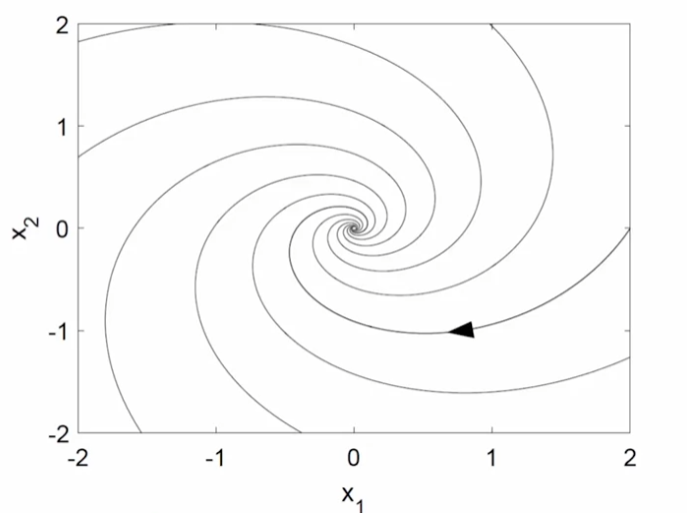
고윳값이 실수가 아닌 복소수가 나타나, 아래와 같이 $X(t)$가 정리될 때 $t$가 변함에 따라 $X_1, X_2$가 회전해 spiral이 나타난다.
\[X(t)=e^{-\frac{t}{2}} \left[A\left(\begin{matrix}\cos{t} \\ -\sin{t}\end{matrix}\right)+B\left(\begin{matrix}\sin{t}\\ \cos{t}\end{matrix}\right)\right]\]
특히, 고윳값의 실수부가 양수이면 바깥으로 발산하고, 음수면 안으로 수렴한다.
spiral의 방향
$x_1=0, x_2=5$ 같은 점에서 $\dot{x}_1$의 부호를 이용해 나선이 clockwise여야하는지, counter clockwise여야 하는지 파악할 수 있다.
Practice Quiz: Phase Portraits
답
1,2,3
Normal Modes
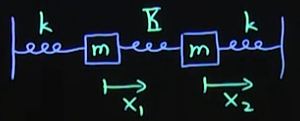
위와 같은 꼴의 Coupled Oscillator이 나타내는 normal modes에 대해 설명한다.
위의 두 물체가 움직이는 꼴을 관찰하면 얼핏 복잡해 보일 수 있으나, 그냥 $(x_1, x_2)$를 관찰하는 대신 $(x_1 + x_2, x_1 - x_2)$를 관찰하면 굉장히 명확하게 운동이 기술된다. 일반물리학 시간에 2개의 진동의 superposition, 중첩으로 운동이 기술된다고 배우지 않았는가?
\[m\frac{d^2}{dt^2}x=\left(\begin{matrix}-(k+K) & K \\ K & (-k+K)\end{matrix}\right)x\]
두 물체의 변위에 대한 운동방정식은 위와 같은 미분방정식의 형태로 나타난다. 참고로 용수철은 어떤 물체의 왼쪽에 붙어있든 오른쪽에 붙어있든 정확히 똑같은 작용을 한다.
위의 미분방정식을 풀어내면, $mr^2v=Av$, $\lambda=-k, -(k+2K)$가 나온다. $mr^2=\lambda$에서 $r=\pm i \sqrt{\frac{k}{m}},\pm i \sqrt{\frac{k+2K}{m}}$이다. 각 고윳값에 대해 고유벡터는 $(1,1)^T, (1,-1)^T$가 나온다.
즉, frequency가 $\sqrt{\frac{k}{m}}$인 $x_1+x_2$에 대한 운동과 frequency가 $\sqrt{\frac{k+2K}{m}}$인 $x_1 - x-2$에 대한 운동으로 전체 운동이 분해되고, 이들의 superposition이 전체 운동이 된다.
Practice Quiz: Normal Modes
답
3,1,3
Week Five Assessment
답
3,4,4,3,3,2,1,3,1,2

