Gumbel Trick Explained
Reparameterization Trick
왜 필요한가?
- deterministic하게 작동하는 NN이라면 상관없지만, VAE처럼 어떠한 stochastic distribution에서 $n$개의 sample을 sampling하여 이후 레이어의 입력으로 삼는 Neural Network의 경우 "sampling 연산"에 대해 gradient를 계산할 수 없다.
- layer의 output $z$를 sampling하는 연산을 Gumbel Distribution을 이용해 argmax로 바꿔버리 자! = Gumbel-Max Trick
- argmax는 미분 불가능하니 softmax로 바꿔주자! = Gumbel-Softmax Trick
Categorical Distribution
$$z \sim \text{Categorical}(\pi_1, \pi_2, \ldots \pi_k)$$
위와 같이 categorical distribution을 따르는 $z$가 있다고 하자. 이 $z$는 $\pi_1$의 확률로 1, $\pi_2$의 확률로 2, ... $\pi_k$의 확률로 $k$가 나온다는 것을 뜻한다.
Cat으로 줄여쓰기도 한다.
Gumbel Distribution
PDF(probability density function): $f(x; \mu, \beta) = \dfrac{1}{\beta}e^{-(z+e^{-z})}, z = \dfrac{x-\mu}{\beta}$
CDF(cumulative distribution function): $F(x; \mu, \beta)=e^{-e^{-z}}, z=\dfrac{x-\mu}{\beta}$
CDF의 역함수: $Q(z)=-\ln(-\ln(z)), z=\dfrac{x-\mu}{\beta}$
$\mu, \beta$는 평균, 표준편차와 관계 없다. 그냥 분포의 parameter라고 보면 된다.
Gumbel-Max Trick
$\text{argmax}(\ln{\pi_i}+z_i), z_i \sim_{i.i.d} \text{Gumbel}(0,1)$ is sampling of $\text{Cat}(\pi)$
다시 말해, $\text{Cat}(\pi)$에서 샘플링하는 것이랑 Gumbel(0, 1)을 따르는 $z_i$에 대해 $\text{argmax}(\ln{\pi_i}+z_i)$을 구하는 게 똑같다. 그 증명은 후술한다.
샘플링 연산이 argmax 연산과 같다니, 상당히 놀라운 결과라고 개인적으로 생각했다.
Proof
Proof: $\text{argmax}(\ln{\pi_i}+z_i), z_i \sim_{i.i.d} \text{Gumbel}(0,1)$ is sampling of $\text{Cat}(\pi)$
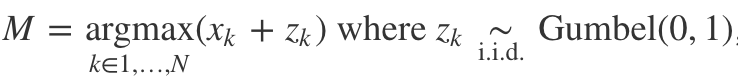
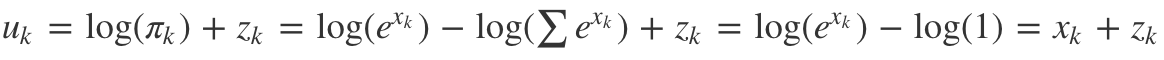

출처: https://medium.com/swlh/on-the-gumbel-max-trick-5e340edd1e01
Gumbel-Softmax Trick
Gumbel-Softmax Trick이 뭐냐?
argmax를 softmax로 바꿔주는 게 전부이다.
더도 말고 덜도 말고 그냥 이게 전부다. 이렇게 해서 sampling 연산을 softmax 연산으로 바꿔버 리고 SGD가 잘 실행되도록 만든다.
다만 딥러닝의 많은 곳에서 softmax distribution의 temperature parameter[1]은 생략해서 쓰는데, Gumbel-Softmax Trick을 소개한 저자들은 temperature parameter을 넣어 학습 과정에 따라 높은 값에서 낮은 값으로 annealing하며 사용한다.
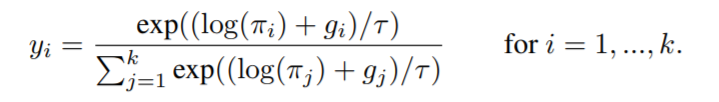
온도 $\tau$가 낮으면 argmax와 같은 연산을 하며 $\tau$가 높으면 uniform sampling과 같은 연 산을 한다.
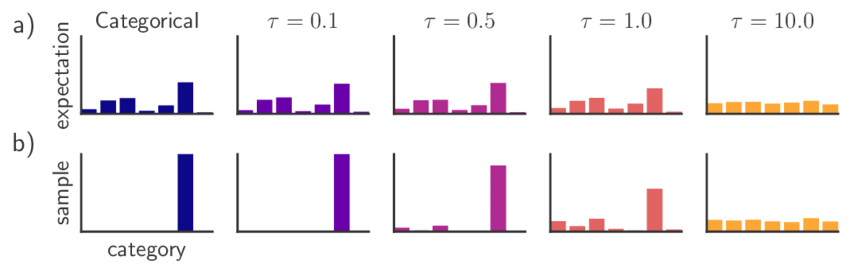
아마 simulated annealing등에서 "온도"를 인자로 넣어줄텐데, 그거랑 비슷한 역할이다. 그리고 물리학에서는 그 원래 알던 온도랑 똑같은 의미다. ↩︎

