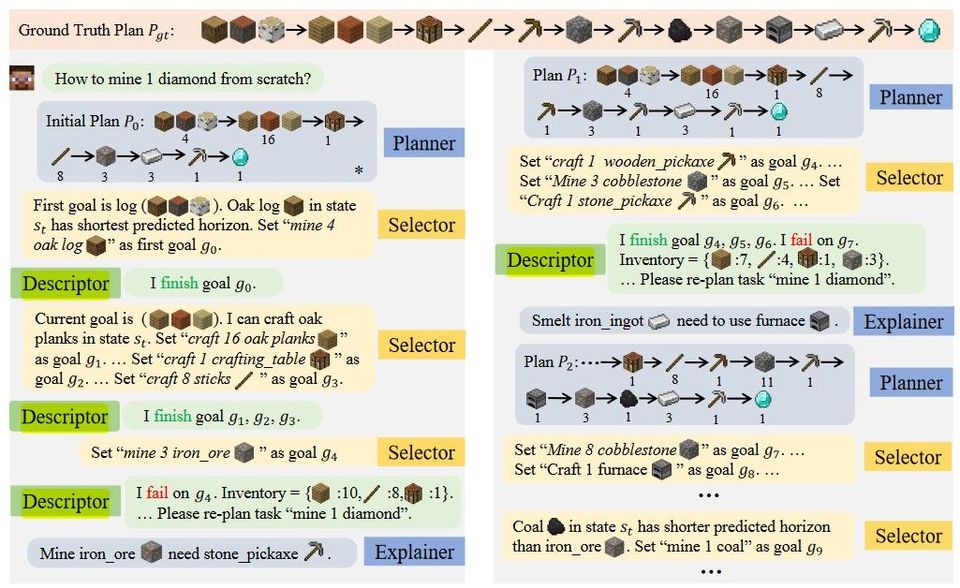
NeRF: Representing Scenes as Neural Radiance Fields for View Synthesis

요약

$(x,y,z,\phi,\theta)$를 입력으로 받아 $(R,G,B,\rho)$를 출력으로 하는 인공신경망을 제시한다.
이미지의 특성 픽셀을 나타내는 ray 위의 모든 $(x,y,z,\phi,\theta)$에 대해 $(R,G,B,\rho)$를 계산하고, 이들을 해당 particle의 밀도($\rho)$와 카메라에서 해당 particle까지 ray가 지나온 매질의 밀도 합 $T(t)$을 이용해 $\hat{\bold C}(\bold r)=\int T(t)\rho(\bold r(t))\bold c(\bold r(t),d)dt$을 계산해 픽셀의 RGB값을 계산한다.
이렇게 하면 임의의 시각에서 scene을 바라봤을 때 카메라에 맺힐 이미지를 예측해낼 수 있다.
이것을 이용해 하나의 scene에 대한 여러 view에서의 2D image를 입력으로 받아 모델을 학습시키고, 학습시키지 않은 view에서 2D image를 예측할 수 있다.
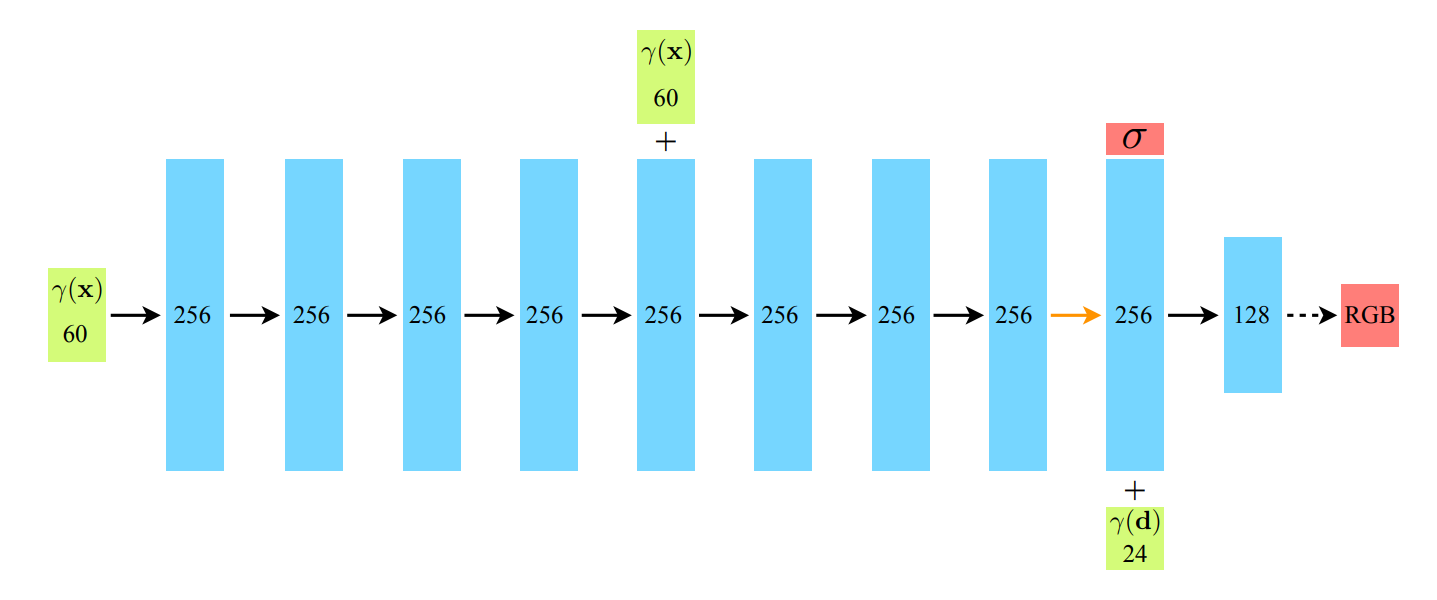
본 논문에서 제시한 신경망은 단순 MLP이다.
수식

ray에 대한 color의 이론적 예측값
적분 꼴로는 직접 계산이 안 되므로 이산적으로 바꿔 계산한다. 점의 sampling은 아래와 같이, 등분한 구간에서 uniform distribution을 추출한다.
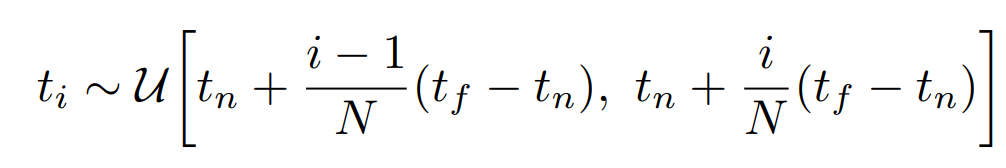
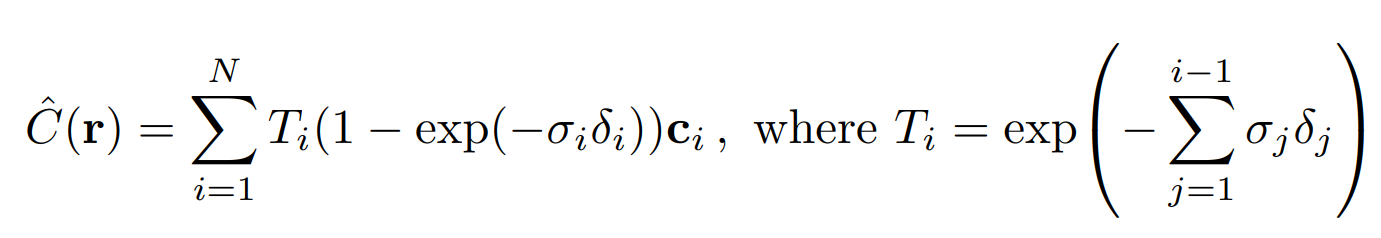
ray에 대한 color 추정값 계산 수식이다.
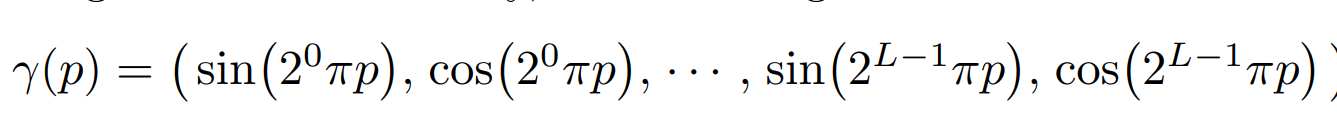
5-dim input을 그대로 넣으면 성능이 그닥 나오지 않고, 위와 같이 positional encoding을 통해 high-dimension, high-frequency로 넣어줘야 글자 등이 잘 나올 정도의 정확도가 확보된다.
관련 후속논문을 첨부한다. Fourier Features Let Networks LearnHigh Frequency Functions in Low Dimensional Domains
Why Exponential decay?
뭔가 대단한 이유가 있나 싶어서 찾아봤는데, 그냥 지수함수에서 지수 부분을 더하는 게 곱셈의 역할을 해서 그렇다. 지극히 당연한 건데 잠깐 생각이 안 나서 찾아봤다..
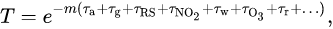
간단히 말하면, 흡수율 곱에 따라 원래는 $a \cdot b \cdot c$형태로 나타내어 지는데 exponential function을 이용해 나타내면 지수의 합으로 나타내면 된다.
그래서 지수쪽에 integral을 넣으면 수식이 성립한다.
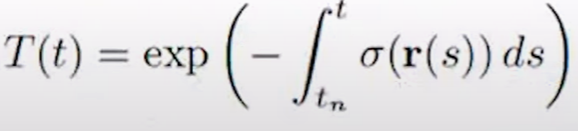
5.2 Hierarchical volume sampling
먼저 coarse하게 sample point들을 추출하고, 그 중에서 가중치가 큰 것이 더 자주 뽑히도록 추가로 sampling을 한다. 원래 sampling된 포인트와 더해 fine network의 입력으로 넣는다.
참고 자료

관련 논문
- Implicit Neural Representations with Periodic Activation Functions: INP with
sinactivation function - NeRF in the wild
- mip-NeRF
- Fourier Features Let Networks Learn High Frequency Functions in Low Dimensional Domains