https://twitter.com/MetaAI/status/1536728499846688768?s=20&t=Sy6-wF8Jaxq1f6FSjrTBGg
https://arxiv.org/abs/2205.14108

이번에 Meta AI에서 재밌어 보이는 논문이 나와 바로 읽어보고 리뷰한다. 다만, 내가 본래 아는 분야가 아니고 흥미 위주로 가볍게 읽고 해설하는 것이기에 오류가 있을 수 있다.

일단, 저자들의 설명에 따르면 Scalable Polynomial Additive Models(SPAM)은 설명이 힘든 DNN과 다르게 완전히 설명이 가능하면서 기존의 설명 가능한 모델보다 뛰어난 성능을 낸다.

Introduction이랑 Related Work는 차치하고, SPAM에 대해 간단히 정리해보겠다.

3. Scalable Polynomial Additive Models

일단 Generalized Additive Models(GAM)는 아래와 같은 형태를 띈다. 교양 통계학에서 선형회귀 를 배울 때 2개의 요인에 대한 '교호작용'을 배웠을 텐데, 그를 일반화한 형태라고 보면 된다. 1. 선형모델이 아니어도 되고 2. order 2가 아닌 order $d$까지 커버한다.

가장 간단한 GAM은 아래와 같이 다항식의 형태를 띈다.

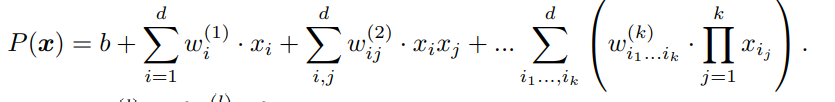
텐서곱 형태로 나타내면 아래와 같다.

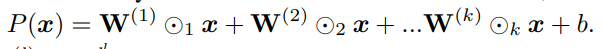
3.1 Learning Low-Rank Decompositions of Polynomials

그리고 특히, 이 때 $\mathbf{W}^{(k)}$는 order $k$의 symmetric tensor이다. symmetric tensor은 쉽게 말해 입력 $(x_1, x_2, \ldots, x_k)$의 permutation에 대해서 모두 똑같은 출력을 내는 텐서이다. 그리고 이러한 symmetric tensor은 rank decomposition이 가능함이 알려져 있다.

다만 저렇게 정보량을 줄여도 되나..? 하는 의문이 좀 들지만 나중에 어차피 여러 인자 교호작용은 조금만 고려해도 된다는 투로 서술이 나온다. 그리고 $k>2$일 때 최대 base $d$개가 아닌 것 같은데 그것도 어차파 적은 개수 쓰니까 상관없을 것 같고. 확실하지는 않지만 최대 $d$개라는 서술은 틀린 것 같은데, 이런 논문에 오류라니 이상하긴 하다. 지금 arxiv 기준 v2인데 나중에 고쳐져 있을수도?

아무튼, SPAM에서는 Propositoin 1을 통해, SPAM이 컨벡스 최적화가 잘 될것이라는 전제를 세운 다.

3.2 Improving Polynomials for Learning

• Geometric rescaling: $x$를 여러 번 곱한 항이 혼재되어 있으면 variance가 안 맞는다. 그를 맞춰주기 위해 기하평균을 사용한다. 그냥 들어서 이상할 부분은 아무것도 없지만 꽤 인상 깊은 처리였다.
• Shared bases for multi-class problems: multi-class problems에 대해 모델을 각 class별로 만들면 $\mathcal{O}(drC)$ weight가 필요하니 텐서의 기저는 공유하고 고윳값만 다르게 학습한다. 이후 softmax를 적용한다.
• Exploring nonlinear input transformations: $\langle u, x \rangle$ 대신 $\langle u, f(x) \rangle$을 사용한다. 이 때 $f$가 Neural Additive Model(NAM)이라는데, 난 뭔지 모르고 이 논 문을 전체적으로 봤을 때 가장 중요한 부분은 아니므로 그냥 넘어가자고 판단했다.
• Dropout for basis via $\lambda$: $\lambda$를 0으로 만들어 일부 basis에 대한 dropout을 실행했다고 한다. 그 영향이 어느정도 되나 궁금한데, 꽤 신기한 아이디어다.

3.3 Approximation and Learning-Theoretic Guarantees

Prop.2를 통해 어느 정도 오차를 감수하고 universal function approximators로 polynomials를 사용할 수 있음을 드러내고, 그 이후 내용은 모델의 수렴성과 관련된 내용으로 보이는데 나에게 주로 관심이 있는 부분은 아니므로 안 읽었다.

4. Offline Experiments

interpretable baselines보다 우수하고 uninterpretable black-boxed baseline과도 어느 정도 경쟁력이 있음을 보여준다.

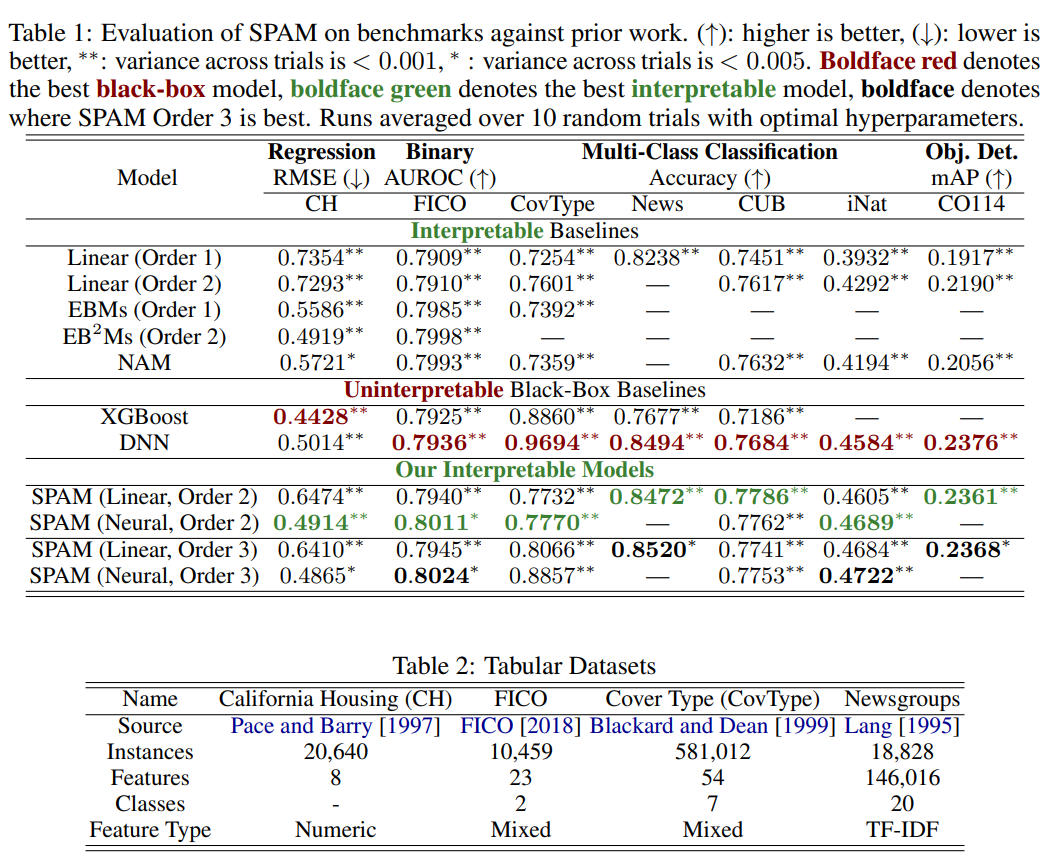
논문의 핵심 아이디어는 (아마도) 이해했다고 봤기에 이후 내용은 안 읽었다. 나중에 내용이 추 가될지도?

뭐 아무튼 DNN 아닌 ML이라니 상당히 흥미로운 내용임에 틀림없다. 근데 기대했던 것보다 생각보다 간단한데.. 이게 성능이 잘 나올까? 하는 생각이 좀 드는데, 많은 사람들이 여러 케이스에 대해 써보면 평가가 나오겠지. 생각보다 간단하긴 해도 새롭다는 것은 확실하다.